در پست قبل از روش اویلر برای حل معادله دیفرانسیل مربوط به نیمه عمر رادیواکتیو استفاده کردیم. تو این پست هم میخوایم دوباره از این روش استفاده کنیم و یک حرکت پرتابی واقعی! رو شبیه سازی کنیم که کمی پیچیده تر از مثال مربوط به رادیواکتویه .
در پست قبل از روش اویلر برای حل معادله دیفرانسیل مربوط به نیمه عمر رادیواکتیو استفاده کردیم. تو این پست هم میخوایم دوباره از این روش استفاده کنیم و یک حرکت پرتابی واقعی! رو شبیه سازی کنیم که کمی پیچیده تر از مثال مربوط به رادیواکتویه .از معادله دیفرانسیل حرکت پرتابی شروع می کنیم. گفتیم که میخوایم حرکت پرتابیمون واقعی باشه، یعنی ما اثر مقاومت هوا رو هم روی جسممون در نظر می گیریم. اما حرکت ما در صفحه انجام میشه و باید معادلاتمون رو به دو راستا (x – y) تجزیه کنیم.
معادله دیفرانسیل های این حرکت بصورت زیر هستند (اگر با معادلات زیر مشکل دارید به کتابهای فیزیک پایه و یا مکانیک کلاسیک (تحلیلی) رجوع کنید) :
$$ \frac{\mathrm{d^2}{x} }{\mathrm{d} t^2}=\frac{F_{d,x}}{m} $$
$$ \frac{\mathrm{d^2}{y} }{\mathrm{d} t^2}=-g + \frac{F_{d,y}}{m} $$
که در این معادلات ${F_{d}}$ اثر مقاومت هواست و با سرعت حرکت جسم بصورت زیر رابطه داره :
$$F_{d}=-\beta v^2 \widehat{v}$$
همونطور که مشخصه معادله های دیفرانسیلمون مرتبه دو هستند. خب این کار مارو سخت نمیکنه، فقط کافیه هر کدوم از این معادلات رو به دو معادله مرتبه اول تبدیل کنیم. یعنی در پایان با چهار معادله دیفرانسیل مرتبه اول سر و کار داریم. حالا اگه ${F_{d}}$ رو هم به دو راستا تجزیه کنیم داریم:
$$F_{d,x} = F_{d} cos{\theta} = F_{d} \frac{v_{x}}{v} = -\beta v v_{x}$$
$$F_{d,y} = F_{d} sin{\theta} = F_{d} \frac{v_{y}}{v} = -\beta v v_{y}$$
و در نهایت چهار معادله دیفرانسیل مورد نظرمون به صورت زیر درمیاد :
$$\frac{\mathrm{{d} x} }{\mathrm{d} t} = v_{x} = f_{x}(t,x,v_{x})$$
$$\frac{\mathrm{{d} v_{x}} }{\mathrm{d} t} = -\frac{\beta}{m} v_{x} \sqrt{v_{x}^2 + v_{y}^2} = f_{vx}(t,x,v_{x})$$
$$\frac{\mathrm{{d} y} }{\mathrm{d} t} = v_{y} = f_{y}(t,x,v_{y})$$
$$\frac{\mathrm{{d} v_{y}} }{\mathrm{d} t} = – g – \frac{\beta}{m} v_{y}\sqrt{v_{x}^2 + v_{y}^2} = f_{vy}(t,x,v_{y})$$
حالا اگه از روش اویلر استفاده کنیم و این معادلات رو گسسته کنیم داریم :
$$x_{i+1} = x_{i} + \Delta t v_{x,i}$$
$$v_{x,i+1} = v_{x,i} – \Delta t \frac{F_{d,x}}{m}$$
$$y_{i+1} = y_{i} + \Delta t v_{y,i}$$
$$v_{y,i+1} = v_{y,i} – \Delta t (g + \frac{F_{d,y}}{m})$$
که در این معادلات t∆ گام گسستهسازی مساله ماست. حالا وقتشه که کد برنامهمون رو بنویسیم . کد این برنامه هم مثل برنامه رادیواکتیو خیلی سادست و نکته اضافی ای نسبت به اون نداره. دوباره به یک ساختار تکرار نیاز داریم که محاسبات رو تا زمانی که پرتابه مون به زمین نخورده( y >= 0 ) ادامه بده و به محض خوردن زمین عملیات رو متوقف کنه.
در ++c:
#include <iostream>
#include <fstream>
#include <math.h>
#define g 9.8
#define B 4e-5
#define m 1.0
using namespace std;
int main()
{
double x, y, vx, vy, v, teta, t, dt = 0.1;
/*** initial conditions***/
t = 0;
x = 0;
y = 0;
v = 100;
teta = 30;
vx = v * cos(teta * M_PI / 180);
vy = v * sin(teta * M_PI / 180);
/***-------------------***/
ofstream o;
o.open("Projectile motion.txt",ios::out);
o<<"x"<<"\t"<<"y"<<"\t"<<"t"<<endl;
while(y >= 0)
{
o<<x<<"\t"<<y<<"\t"<<t<<endl;
v = sqrt(vx * vx + vy * vy);
x = x + vx * dt;
y = y + vy * dt;
vx = vx - (B/m) * v * vx * dt;
vy = vy - g * dt - (B/m) * v * vy * dt;
t += dt;
}
o.close();
}
در قسمت اول برنامه کتابخونه هایی که لازم داریم رو تعریف کردیم. کتابخونه math.h توابع مثلثاتی مثل sin و cos و همچنین یک سری از عملیات های ریاضی مثل جذر و یا به توان رسوندن رو شامل میشه (البته کلی توابع دیگه هم تو این کتابخونه هست!) و چون در بدنه برنامه نیاز به محاسبات ریاضی داشتیم از این کتابخونه استفاده شد. در خطوط بعد، ثوابت مورد نیاز در برنامه رو تعریف کردیم. همونطور که مشخصه در قسمت بعد و در بدنه اصلی برنامه، ابتدا شرایط اولیه رو که شامل مکان ابتدایی جسم، سرعت اولیه و زاویه پرتاب میشه تعریف و بعد سرعت رو به راستای افقی و عمودی تجزیه کردیم. در مرحله بعد فایلی برای ذخیره خروجی درست شد و بعد از اون الگوریتم اویلر برای حرکت پرتابی رو با استفاده از ساختار تکرار while پیاده کردیم.
و در پایتون:
from math import *
g = 9.8
m = 1.0
B = 4e-5
x = 0
y = 0
v = 100
teta = 30
t = 0
dt = 0.1
vx = v * cos(teta * pi / 180)
vy = v * sin(teta * pi / 180)
f = open("Projectile motion.txt", "w")
f.write("x" + "\t" + "y" + "\t" + "t" + "\n")
while y >= 0 :
f.write(str(x)+"\t"+ str(y)+ "\t" + str(t) + "\n")
v = sqrt(vx * vx + vy * vy)
x = x + vx * dt
y = y + vy * dt
vx = vx - (B/m) * v * vx * dt
vy = vy - g * dt - (B/m) * v * vy * dt
t += dt
f.close()
قبل بررسی نمودار حرکت پرتابیمون بیاین پیش بینی کنیم که شکل حرکت چجوری میشه؟! خب در موقع بالا رفتن جسم، نیروی مقاوت هوا و نیروی وزن هر دو به سمت پایین هستن. اما در موقع برگشت، نیروی مقاومت هوا رو به بالا و نیروی وزن روبه پایینه و این یعنی برآیند نیرو های وارد به جسممون در رفت و برگشت فرق میکنه. حالا به نمودار زیر توجه کنین.
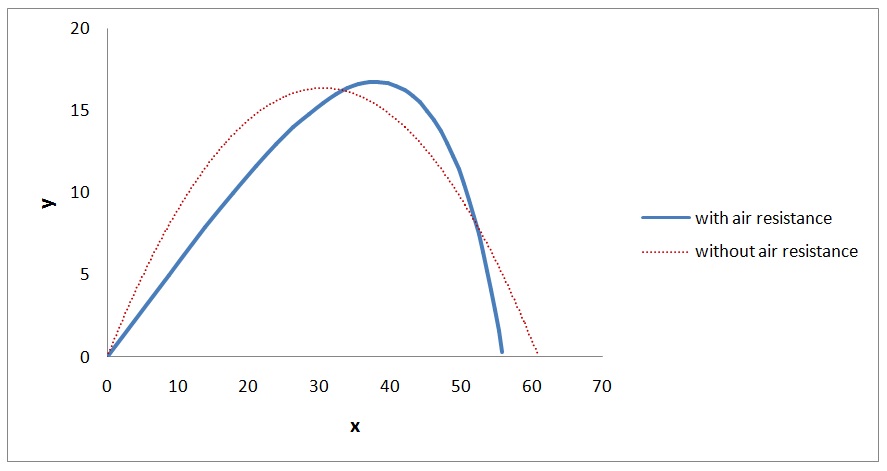
همونطور که انتظار داشتیم، نمودارمون بطور کامل سهموی نیست و تقارن لازم رو نداره و این بخاطر وجود مقاومت هوا در برابر حرکت جسم ماست. مساله دیگه ای که وجود داره، برد پرتابه است. در حالت عادی و بدون مقاومت هوا میدونستیم که همیشه به ازای زاویهی پرتاب 45 درجه برد پرتابه بیشینه میشه. اما با وجود مقاومت هوا دیگه اینطوری نیست.
برای تمرین بیشتر می تونین برنامه ی حرکت پرتابی رو طوری تغییر بدین که به ازای یک سرعت اولیه، برد بیشینه رو برامون پیدا کنه . همچنین میشه برای یک زاویه خاص، سرعتی که در اون زاویه برد بیشینه میشه رو بدست آورد.
در این پست هم یک معادله دیفرانسیل رو با روش اویلر حل کردیم. بازهم این پرسش مطرحه که همه ی معادله های دیفرانسیل با این روش حل میشه یا نه؟ و آیا روش های قدرتمند تر و مطمعن تری هم برای حل معادله دیفرانسیل وجود داره؟
به امید خدا پست بعد فضای متفاوت تری خواهد داشت ، اما در پست های بعدتر، باز هم به حل معادله دیفرانسیل و روش های مختلف برای حل این معادلات بر می گردیم.