سال‌ها بود که بشر به بسیاری از معادلات سخت ریاضی و ارتباط تنگاتنگشان با علومی مانند فیزیک رسیده بود. اما نکته خیلی مهمی وجود داشت و آن انجام این محاسبات و کشف و بررسی پدیده‌های طبیعی مرتبط با آنها بود. در بسیاری از موارد، انجام یک عملیات ساده ریاضیاتی ساعت‌ها و حتی روزها از دانشمندان وقت میگرفت و زمان مهمترین مساله به حساب می‌آ‌مد. انسان آن روزها به این فکر افتاد که چگونه می‌تواند این حجم وسیع از محاسبات را در زمان کمتر انجام دهد! و از همان روزها، اولین جرقه براي ساخت وسیله‌ای که بعدا به آن کامپیوتر گفتند زده شد. در سال 1937 میلادي اولین نسل از رایانه‌ها ساخته شد. البته قبل از این سال هم تلاش‌های موفقی در زمینه‌ی ساخت دستگاه‌های محاسباتی انجام شده بود. شاید کسی در آن زمان فکرش را نمی‌کرد رایانه‌ها تا حد امروزی بتوانند پیشرفت کنند. طوری که امروزه نمی‌توانیم نقش اساسی آن را در زندگی در نظر نگیریم. اما اگر از آن دوران بگذریم و برسیم به زمان خودمان، می‌بینیم به‌طور تخصصی در زمینه فیزیک، کامپیوترها نقش و جایگاه ویژه‌ای پیدا کرده‌اند که روز به روز در حال پررنگ‌تر شدن می‌باشد. شبیه سازی‌های گسترده‌ای که در فیزیک انجام میشود، محاسبات فیزیکی، طراحی آزمایشهای متنوع فیزیکی و . . . نمونه‌های کوچکی از کاربردهای کامپیوتر در فیزیک به حساب میآید.
قصد دارم طی چند پست از کاربردهای مختلف کامپیوتر در فیزیک صحبت کنم و نمونه‌هایی از شبیه سازی‌ها، تحلیل داده‌ها و کمی هم پردازش تصویرهای انجام شده در فیزیک را مورد بررسی قرار دهم.
براي برنامه‌نویسی چه‌کار کنیم؟
خب با زبان‌های مختلفی میتوانیم برنامه‌مان را بنویسیم. در اینجا براي نمونه از دو زبان برنامه نویسی استفاده میکنیم : ++C و Python و برنامه‌هایمان را با هر دو زبان می‌نویسیم. البته هرجا که نیاز باشد از نرم‌افزارهای دیگر هم حتما استفاده میکنیم تا با طیف گسترده‌تری از برنامه‌های کاربردی آشنا شویم. درواقع ++c که پیشرفته شده زبان c هست، یک زبان همه منظوره است که امکان برنامه نویسی شئ‌گرا جزو ویژگی‌های اصلی آن به حساب میآید و یک زبان برنامه نویسی با سطح میانی به حساب میآید. براي نوشتن کدها به زبان ++C میتوان از نرم افزار هاي مختلفی استفاده کرد. در سیستم عامل ویندوز نرم افزارهایی مثل ++Code Blocks، Dev C و Visual studio را شاید بتوان به عنوان ساده ترین و پرکاربردترین نرم‌افزارهای برنامه نویسی به زبان سی پلاس پلاس معرفی کرد. در توزیع‌های گنو/لینوکس به سادگی میتوان کدهای مورد نظر را در هر نرم‌افزار ویرایش‌گر متنی مانند gedit (در دسکتاپ گنوم) نوشت و در ترمینال اجرا کرد. (یا مثلا اینکه از نرم افزار geany استفاده کرد). اما در مورد پایتون باید گفت یکی از ساده ترین، پرکاربردترین و محبوب‌ترین زبان‌های برنامه‌نویسی به حساب میآید. دارای محیطی بسیار ساده و دلنشین است که ارتباط برقرار کردن با آن بسیار راحت می‌باشد. برای اطلاعات بیشتر به وب‌سایت پایتون رجوع بفرمایید.
برویم سراغ یکی از ساده‌ترین و تقریبا مهمترین مباحث موجود در فیزیک: حل معادله دیفرانسیل. در بسیاری از مسائل فیزیکی(کلاسیک و غیرکلاسیک)، به یک معادله دیفرانسیل برخورد میکنیم. اگر سري به کتاب‌های آموزشی معادلات دیفرانسیل بزنید، راه‌های تحلیلی زیادی براي حل این معادلات پیدا خواهید کرد. از راه حل‌های ساده گرفته تا راه‌های پیچیده و دشوار. در اینجا میخواهیم به معرفی روش‌هایی که بتوان به‌سادگی بسیاری از معادلات دیفرانسیل را به صورت عددی (با کامپیوتر و برنامه نویسی) حل کرد، بپردازیم. در ضمن نکته بسیار مهمی که باید ذکر کنیم این است که بسیاری از معادله‌های دیفرانسیل جواب تحلیلی ندارند! و استفاده از روش‌های عددی تنها راه حل به حساب میآید.
روش حل عددی چیست!؟
در روش‌های عددی مساله را بجای اینکه پیوسته در نظر بگیریم(مانند حل تحلیلی)، گسسته فرض میکنیم سپس در بازههای زمانی کوچک جواب مساله را به دست می‌آوریم و مساله را با تقریب زدن ساده ترش میکنیم. اینکار را بارها تکرار میکنیم تا به جواب مورد نظرمان برسیم. براي انواع معادلات دیفرانسیل، انواع روش‌های عددی وجود دارد مثل : روش اویلر ، روش اویلر-کرامر، روش هون ، روش تیلور، روش رانگ-کوتا ، روش آدامز-بشفورت-مولتون و … .
با یک مثال ساده فیزیکی شروع کنیم:
می خواهیم نیمه عمر یک ماده رادیواکتیو را بررسی کنیم. نیمه عمر به مدت زمانی می‌گویند که ماده پرتوزا به نصف مقدار اولیه‌ی خود بر اثر واکنش‌های پرتوزایی تقلیل پیدا می‌کند. معادله دیفرانسیل مربوط به نیمه‌عمر رادیو اکتیو را میتوان بصورت زیر نوشت:
$$ \frac{\mathrm{d}N(t) }{\mathrm{d} t}=-\frac{N(t)}{\tau} $$
در این معادله ${N(t)}$ تعداد ذرات ماده برحسب زمان و τ طول عمر متوسط ماده‌ی پرتوزا است.${N(0)}$ مقدار اولیه ماده‌است و τ برای اورانیوم ۲۳۵ برابر با ۷۰۰میلیون سال است. حل تحلیلی این معادله به صورت زیر می‌باشد:
$$N(t)=N_0 e^{-t/\tau }$$
حالا میخواهیم این معادله را گسسته کنیم و در بازههای زمانی کوچک حلش کنیم و در نهایت حل عددی آن را با جواب تحلیلی مقایسه کنیم. ابتدا بسط تیلور تابع${N(t)}$ را می نویسیم:
$$N_{(t)}=N_0 +\frac{\mathrm{d}N_{(t)} }{\mathrm{d} t}\Delta t+ \frac{1}{2}\frac{\mathrm{d^2}N_{(t)} }{\mathrm{d} t^2}\Delta t^2+…$$
خب در بسط تیلور، هرچقدر t∆ کوچکتر باشد تقریب دقیق‌تری داریم (زیرا گسستگی کمتر میشود) و حتی میتوانیم جملات از مرتبه 2 به بعد را هم نادیده بگیریم.زیرا هرچقدر t∆ کوچکتر باشد، در عمل وقتی به توان میرسد قابل چشم پوشی است. در نتیجه به معادله زیر میرسیم:
$$N_{(t)}\approx N_0 +\frac{\mathrm{d}N_{(t)} }{\mathrm{d} t}\Delta t $$ $$ \frac{N_{(t)}-N_0}{\Delta t}\approx \frac{\mathrm{d}N_{(t)} }{\mathrm{d} t}$$
$$\frac{\mathrm{d}N_{(t)} }{\mathrm{d} t}=\lim_{\Delta t\to 0}{\frac{N_{(t+\Delta t)}-N_{(t)}}{\Delta t}}$$
پس میتوانیم به راحتی نتیجه بگیریم :
$$N_{(t+\Delta t)}\approx
N_{(t)}+\frac{\mathrm{d}N_{(t)} }{\mathrm{d} t}{\Delta t}$$
این معادله در واقع مقدار تابع مورد نظر را در هر مرحله نسبت به مرحله قبل به ما میدهد (به اندیس ها توجه کنید).طبق معادله دیفرانسیل مربوط به نیمه عمر رادیواکتیو هم میدانیم${ \frac{\mathrm{d}N(t) }{\mathrm{d} t}=-\frac{N(t)}{\tau} }$ و در نهایت میرسیم به یک معادله تر و تمیز برای برنامه نویسی و محاسبه عددی:
$$N_{i+1}\approx
N_{i}-\frac{N_{i} }{\tau }{\Delta t}$$
به این روش گسسته‌سازی معادله دیفرانسیل، روش اویلرمی‌گویند.
خب تنها کاري که باید براي نوشتن برنامه انجام دهیم پیاده کردن الگوریتم اویلر است . خب اطلاعاتی که در اختیار داریم چیست؟ مقدار اولیه ماده (شرایط اولیه)، معادله دیفرانسیل مربوطه و گام گسسته‌سازی یا همان t∆ . کاري که باید بکنیم این است که${N_{i+1}}$ را نسبت به مرحله قبل حساب و مقدار آن را در هر مرحله ذخیره کنیم. پس در واقع ما به یک ساختار تکرار نیازمندیم که در هر مرحله زمان و ${N_{i+1}}$ را برایمان حساب و ذخیره کند. یک سری کارهای جانبی هم می‌ماند مثل تعریف متغیرها ، اضافه کردن کتابخانه ها (در زبان ++c) و … که کارهای ساده‌ا‌ی هستند.
در ++c:
#include <iostream>
#include <fstream>
using namespace std;
int main()
{
double N, dt = 0.01, T = 700, t = 0;
N = 100;
ofstream o;
o.open("Radioactive Decay.txt", ios::out);
o<<"Time"<<"\t"<<"Numerical"<<endl;
while(t <= 20)
{
o<<t<<"\t"<<N<<endl;
N = N - (N / T) * dt;
t = t + dt;
}
o.close();
}
و در پایتون:
t = 0 T = 700 N = 100 dt = 0.01 f = open("Radioactive Decay.txt", "w") f.write("Time" + "\t" + "Numerical" + "\n") while t <= 20 : N = N - ( N / T ) * dt t = t + dt f.write(str(t) + "\t" + str(N) + "\n") f.close()
سعی کردیم برنامه‌ها را در نهایت سادگی بنویسیم! در قسمت اول برنامه، متغیرهای مورد نیاز را تعریف کردیم و مقدارهاي اولیه را به آنها نسبت دادیم. سپس یک فایل ایجاد کردیم تا اعداد محاسبه شده را در آن ذخیره کنیم. قسمت بعد با استفاده از یک دستور تکرار، الگوریتم اویلر را پیاده و اعداد را در فایلی که قبلا ایجاد کرده بودیم، ذخیره کردیم . حالا ما از این اعداد استفاده میکنیم و نمودارهاي مساله مورد نظرمان را رسم میکنیم.
در نمودارهای زیر حل تحلیلی و عددی را با هم مقایسه و درصد اختلاف آنها را با توجه گام گسسته‌سازی مقایسه کرده‌ام. به این نکته هم باید توجه کرد که شرایط اولیه مساله کاملا دلخواه است و میتوان مساله را به ازای شرایط اولیه مختلف حل و جواب‌ها را مقایسه کرد.
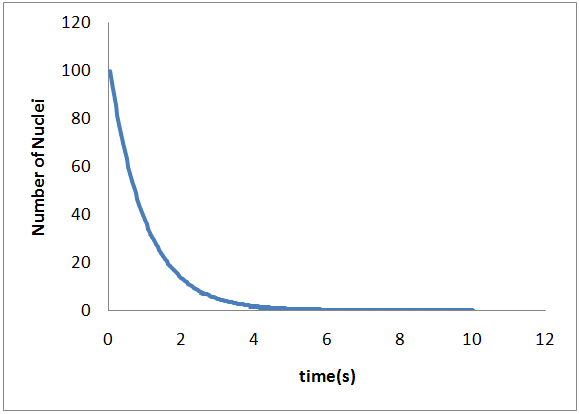
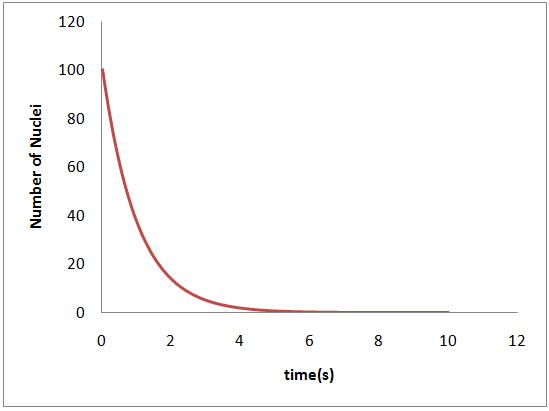
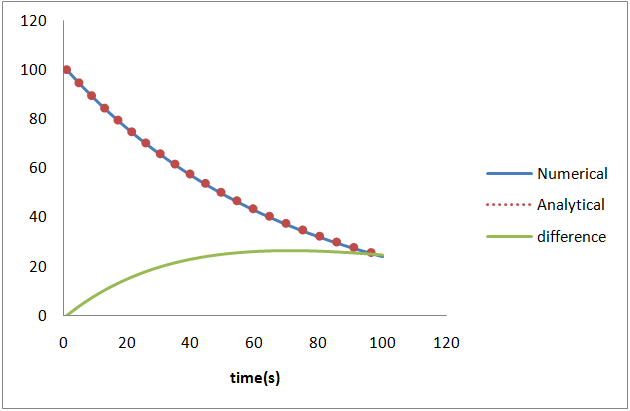
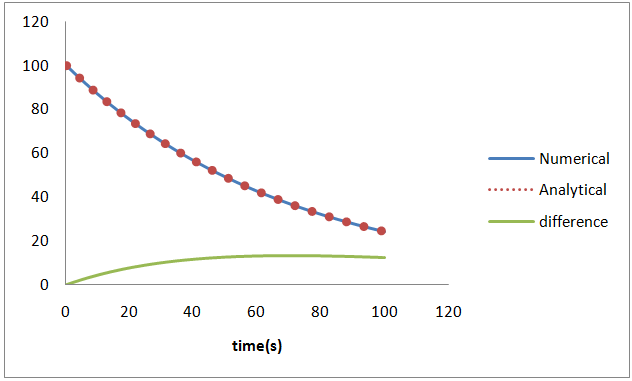
می‌بینیم که طبق انتظارمان حل تحلیلی و حل عددی بسیار به هم نزدیک هستند و با کاهش گام گسسته سازی جواب تحلیلی و عددی بسیار بهم نزدیک می‌شوند. معادله‌های دیفرانسیل زیادي را میتوان به همین سادگی حل کرد. میتوان از بخش گرافیکی خود محیط برنامه‌نویسی هم استفاده کرد و نمودارها را در همان محیط برنامه‌نویسی رسم کرد (به زودی در مورد آنها هم می‌نویسم). همچنین میتوان خروجی برنامه را برای تحلیل‌های دقیق‌تر و کارهای جالب و هیجان انگیز دیگر، به نرم‌افزارهای ریاضیاتی پیشرفته مثل Methematica داد.
چند سوال باقی می ماند: آیا همه معادلات دیفرانسیل را میتوان با این روش حل کرد؟ اگر معادله دیفرانسیل مرتبه یک نباشد حل عددی آن چگونه میشود؟ حل‌های عددی برای هر مقدار اولیه و هر گام گسسته سازی دارای جواب قابل قبول هستند؟ به امید خدا در پستهای بعدي این سوالات را بررسی خواهیم کرد.
- منابع
- http://en.wikipedia.org/wiki/History_of_computing_hardware http://en.wikipedia.org/wiki/Python_(programming_language)
- http://en.wikipedia.org/wiki/C%2B%2B Nicholas J Giordano_ Hisao Nakanishi-Computational physics-Pearson_Prentice Hall (2006)
سلام
مطلب عالي بود – توضيحاتي شفاف و مفيد كه در هيچكدام از كلاسهاي معادله ديفرانسيل يا محاسبات يا حتي اجزاي محدود تا حالا نشنيده بودم
تشكر بسيار
[…] چگونه‌ازكامپيوتردرفيزيک‌استفاده‌كنيم؟ این قسمت: حل … […]
[…] شده کد توی متلب بزنه اسمش نیست مهندسی برق. اسمش هست حواشی رشته برق که تو اکثر مهندسی‌های دیگه و حتی علوم پایه هم […]