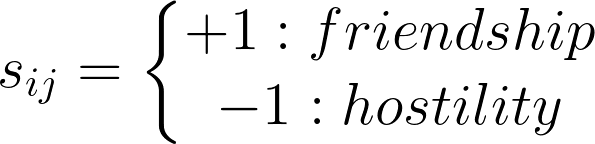یاد دارم در جایی ریچارد فاینمن، بزرگترین معلم فیزیک، میگفت: «معلم زمان تدریس، مانند یک بازیگر روی سن است. او باید بتواند با تمام هنرش مخاطب را درگیر یادگیری کند.» آنچه کلاس درس فاینمن را از مابقی کلاسها متمایز میکرد یقینا همین درگیر کردن مخاطب با یادگیری است. در ادامه نوشته قبل در باب معرفی ساختوسازگرایی میخواهم تجربهای از شرکت در دو برنامه کمدی (جُنگ) که از ساعت ۱۲ شب شروع و تا ۴ بامداد ادامه داشت استفاده کنم و به کمک آن از ساختوسازگرایی دفاع کنم. البته که این قیاسی معالفارق است، با این وجود آنچه مورد اشاره است درگیر کردن مخاطب است.
هدف اصلی آموزش، یادگیری است. اما نه آنگونه که رفتارگرایان از آن یاد میکنند. رفتارگرایانی از قبیل جان واتسون و اسکینر سرشت انسان را انعطافپذیر میدانستند، و معتقد بودند که در رشد، یادگیری نقش اصلی را ایفا میکند، چنانکه آموزش اولیه میتواند صرفنظر از آنچه کودک از استعدادها، تمایلات، علاقهها، تواناییها، نژاد و اجداد به ارث برده، او را به هر نوع بزرگسالی تبدیل کند. منظور من از یادگیری در این نوشته، عبارتست از تغییر نسبتاً پایدار در احساس، تفکر و رفتار فرد که بر اساس تجربه و طی یک فرایند جذب و هضم ایجاد شده باشد و البته بتواند توسعه پیدا کند.

هر دو جُنگی که در آن شرکت کرده بودم، ساعت ۱۲ شب شروع میشدند، زمانی که اکثر شرکتکنندهها خسته بودند و گمان من بر این بود که عدهی کمی از آنان (از جمله خودم) تا آخر برنامه حضور خواهند داشت. با این وجود آنچه که مشاهده کردم چیز دیگری بود! نه تنها از تعداد شرکتکنندهها کم نشد بلکه شور و اشتیاق آنان رفتهرفته زیاد هم شد، به دیگرسخن، تمام شرکتکنندهها با وجود تفاوتها و پیشزمینههایی که داشتند در طی برنامه کاملا درگیر شده بودند. پس از جُنگ این سوال برای من پیشآمد که پس چرا ما مدام سر کلاسهای درس چرت میزنیم و کل روز منتظر این میمانیم که کلاس بعدیمان شروع شود تا بتوانیم به چرت نیمهکارهی قبلیمان ادامه دهیم در حالی که به مدت ۴ ساعت، در نیمه شب با تمام خستگی روی یک صندلی نشستیم و با برنامه به خوبی همراهی کردیم؟
پر واضح است که برنامه این گونه جُنگها از قبل مشخص شده است و تمرین زیادی برای اجرای آن به بهترین شکل صورت گرفته است؛ با این وجود در طی برنامه مجری این جنگ با توجه به بازتابهای مختلفی که به صورتهای مختلف از مردم میگرفت برنامهای که البته پر از انعطاف و محل خلاقیت و حاضرجوابی بود را تغییر میداد. به طور مثال، مجری ابتدای برنامه گفت هر جا من فلان حرف را زدم شما بهمان پاسخ را بدهید (محرک) و طی برنامه، با توجه به شدت پاسخی که از مردم میگرفت متوجه میشد که چقدر مردم درگیر آن قسمت از برنامه شدهاند. درست مانند معلمی که هدفش از طرح سوال و یا آزمون سنجش میزان درگیر شدن کلاس با موضوع است. البته مجری جنگ روشهای دیگری هم داشت که به معنی نیاز به محرکهای متنوع در شرایط مختلف است. در جُنگ، شرکتکنندهها از شهرهای مختلف و پیشینهی فکری کاملا متفاوتی حضور داشتند. تلاش مجری در این بود که همه افراد را با توجه به تمام تنوعی که در آنها وجود دارد و سابقه فکری آنها درگیر کند که اگر این گونه نبود غیر ممکن بود تمام افراد آن سالن تا انتهای برنامه در جُنگ باقیبمانند.
ادعای ساختوسازگرایان در مسئله تدریس نیز همین است. معلم باید با توجه به پیشزمینهی دانشآموزان که هر کدام با دیگری تفاوت دارد کلاس درس را ارائه کند و مسیر آموزش را به گونهای پیش ببرد که همه افراد بتوانند درگیر شوند و پس از اتمام کلاس در سطح بالاتری از یادگیری قرار گرفته باشند. از سوی دیگر با اینکه مجری جُنگ مسئولیت مدیریت برنامه را به عهده داشت، در کل برنامه مخاطب را برآن میداشت تا چگونگی پیشروی و انتخاب موضوعات را مشخص کنند. هر چند که وی از زیرکی خاصی برای بیان موضوعات در ترتیب معینی بهره میجست، با این وجود شیوهی مدیریت برنامه بر آن اصل استوار بود که شرکتکنندگان بگویند قسمت بعدی چه باشد. دیدگاه ساختوسازگرایی در آموزش هم بر همین پایه است. به این معنا که معلم باید دانشآموزان را فعالانه و هدفمند در مسیر آموزش قرار دهد و با وجود آزادی که در اختیار آنان قرار میدهد، فعالیتهایی مطرح کند که آنان بتوانند به راحتی در آنها شرکتکنند و خود را مالک ایدههای مطرح شده بدانند. چنانکه این رغبت درآنان به وجود آید که ایدهای که مطرح کردهاند را توسعه و بهبود بخشند. در تمام مسیر، معلم باید با دقت و مهارت زیادی بحث را کنترل کند به طوری که کلاس در انتهای جلسه، همگرا به چیزی شود که معلم انتظار دارد.

در هر دو جنگی که شرکت کرده بودم، از هر وسیله و اسبابی از جمله سازهای مختلف، نورپردازیها مهیج و مهارتهای فردی متفاوتی استفاده میشد تا بر اشتیاق شرکت کنندگان به درگیر شدن در برنامه بیفزایند. همین طور شیوه تحول برنامه به این گونه بود که به مخاطب القا میشد که هر چه بماند احتمالا برنامه مهیج دیگری نیز وجود دارد چرا که مجری برنامه چیزهای زیادی در چنته دارد! درست مانند نگاه ساختو سازگرایان به نقش معلم. در ساخت و سازگرایی معلم باید بکوشد از هر گونه وسیله و ابزاری که به یادگیری کمک میکند در مسیر آموزش استفاده کند و فقط به تخته سیاه و گچ اکتفا نکند. از طرف دیگر معلم باید اطلاع نسبی خوبی از مباحث مرتبط با موضوع درس و مطالب علمی در سطح بالاتر از موضوع مطرح شده هم داشته باشد تا در صورت نیاز، ایده و پاسخ گویاتری به دانشآموزان بدهد. از طرف دیگر، مهارت فوقالعاده زیاد مجری در اداره جنگ را نباید فراموش کرد؛ به این معنی که معلم نیز شدیدا نیاز به توسعه حرفهای دارد و باید برای تدریسش تمرین، دقت و زکاوت زیادی به خرج دهد.
در نهایت با این که کلاس درس تفاوتهای اساسی با یک جنگ دارد، ولی آنچه مهم است شیوهی درگیر کردن مخاطب به کمک رهیافت ساخت و سازگرایی است. چیزی که ما در کلاس درس به دنبال آن هستیم یادگیری است، اگر قرار باشد روشی بیشترین یادگیری را نتیجه دهد، قطعا بهترین روش است!


 این پست، اشارهی مستقیمی دارد به مقاله «استفاده از ساختهای نظری برای تدریس آگاهانه»
این پست، اشارهی مستقیمی دارد به مقاله «استفاده از ساختهای نظری برای تدریس آگاهانه»





 راس ایجاد میکنه. بعد از اون، در هر مرحله، راسی اضافه میشه و به
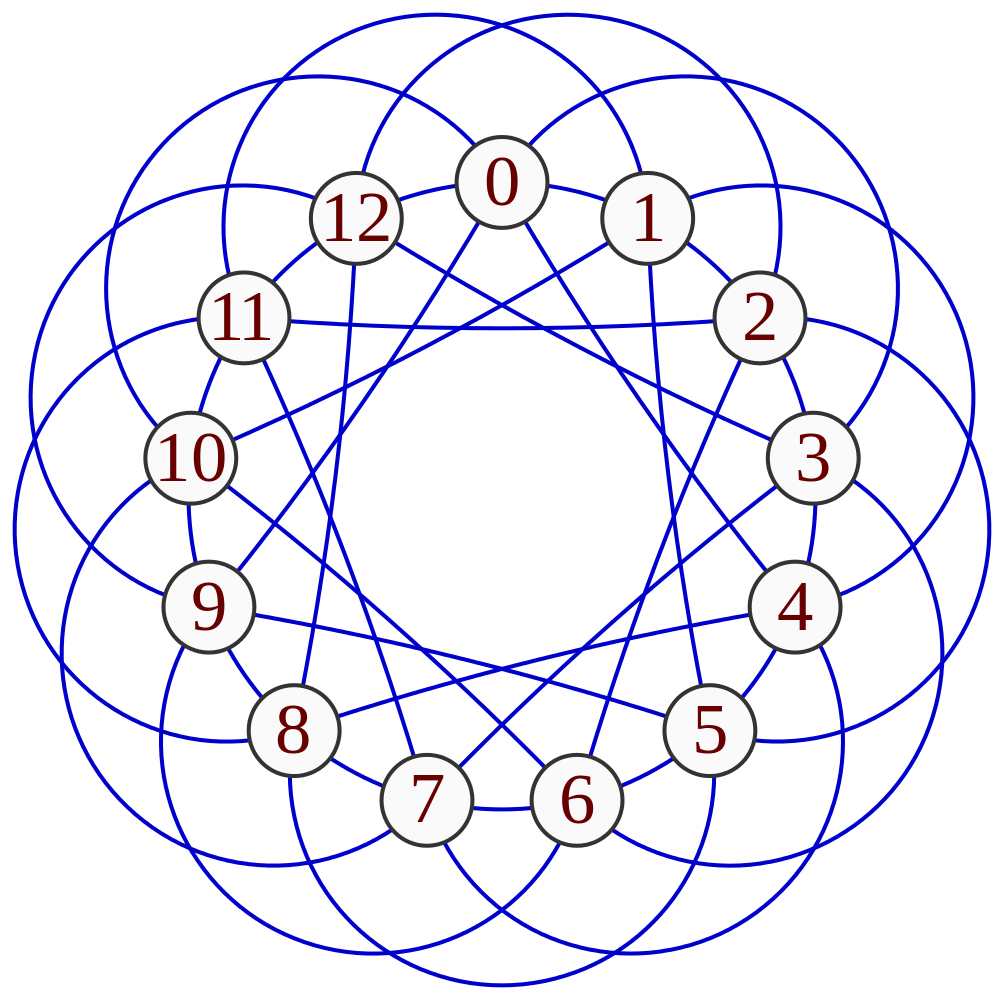
راس ایجاد میکنه. بعد از اون، در هر مرحله، راسی اضافه میشه و به 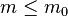 راس قبلی وصل میشه. این m راس بر اساس درجهشون انتخاب میشند: یعنی احتمال اینکه راس جدید به iامین راس موجود درگراف وصل بشه برابره با نسبت درجه راس iام به مجموع درجات کل رئوس. این سبب میشه که «هاب» در شبکه بهوجود بیاد. هابها رئوسی هستند که درجه شون از بقیه رئوس شبکه بیشتره. (صفحه شجریان در اینستاگرام یک هاب به حساب میاد در بین خوانندهها همونجوری که گوگل یک هابه در بین سایتها!). يادتون باشه که در مدل باراباشی-آلبرت وزن هر یال ۱ است!
راس قبلی وصل میشه. این m راس بر اساس درجهشون انتخاب میشند: یعنی احتمال اینکه راس جدید به iامین راس موجود درگراف وصل بشه برابره با نسبت درجه راس iام به مجموع درجات کل رئوس. این سبب میشه که «هاب» در شبکه بهوجود بیاد. هابها رئوسی هستند که درجه شون از بقیه رئوس شبکه بیشتره. (صفحه شجریان در اینستاگرام یک هاب به حساب میاد در بین خوانندهها همونجوری که گوگل یک هابه در بین سایتها!). يادتون باشه که در مدل باراباشی-آلبرت وزن هر یال ۱ است!