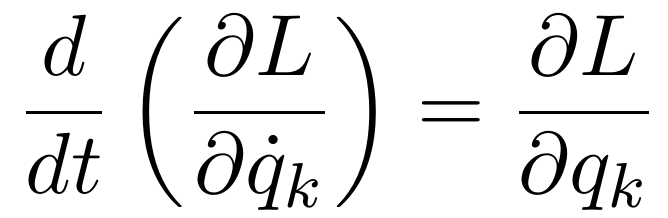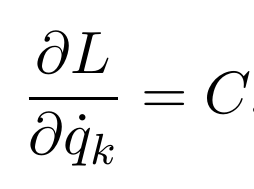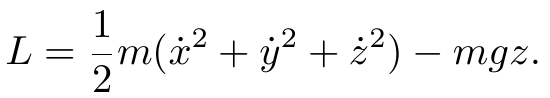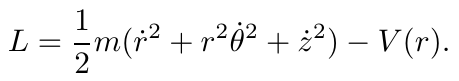لطفا قبل از شروع این پست، پست «ترجمه بهترین آثار کوتاه فاینمن!» را بخوانید. ترجمه این مقاله کاری از گروه ترجمه دانشجویان فیزیک امیرکبیر است. شما میتواند این مقاله به صورت فایل pdf دانلود کنید.
لطفا قبل از شروع این پست، پست «ترجمه بهترین آثار کوتاه فاینمن!» را بخوانید. ترجمه این مقاله کاری از گروه ترجمه دانشجویان فیزیک امیرکبیر است. شما میتواند این مقاله به صورت فایل pdf دانلود کنید.
ویدیوی لذت درک امور:
من دوست هنرمندی دارم، او بعضی اوقات دیدگاه هایی دارد که من زیاد با آن ها موافق نیستم. مثلا گلی را به دستش می گیرد و می گوید: « ببین چقدر زیباست » و من هم با او موافقم، در ادامه می گوید « می بینی، من به عنوان یک هنرمند زیبایی گل را می بینم. اما تو به عنوان یک دانشمند، آن را تکه تکه می کنی و از بین می بری». به نظر من او یک جور دیوانه است. اولا من معتقدم آن زیبایی را که او می گوید همه می توانند ببینند، از جمله من، شاید زیبایی شناسی من به اندازه او قوی نباشد ولی برای من هم زیبایی گل تحسین برانگیز است. و این در حالی است که من در مورد گل چیزهای بیشتری میبینم. من سلول ها و واکنش ها پیچیدهای که درون آنها اتفاق می افتد را می توانم تصور کنم و آنها هم به نوبه خود دارای زیبایی هستند. منظورم اینست که زیبایی فقط در ابعاد سانتی متری نیست و در ابعاد کوچکتر و در ساختارهای داخلی نیز زیبایی وجود دارد. همچنین در فرآیندهای داخلی این گل رنگ ها طوری آمیخته شده اند که حشرات را برای گرده افشانی جذب کنند. و این فرآیند جالبست چون این را نشان می دهد که حشره ها هم رنگ را می بینند. یک سوال پیش می آید: آیا این حس زیبایی شناسی در ساختارهای ریزتر هم وجود دارد؟ چرا زیباست؟ تمامی این سوالات گوناگون و جالب نشان می دهد که دانسته های علمی به هیجان، رموز و هیبت یک گل اضافه می کند؛ نمی توانم بفهمم که چگونه کاهش می دهد.
اجتناب از دروس علوم انسانی
من همواره آدمی تک بعدی بوده ام و فقط در جهت علمی تلاش می نمودم و در زمان جوانی تمام تمرکزم بر روی این یک بعد بود. وقت و حوصله زیادی برای یاد گرفتن چیزی که علوم انسانی نامیده می شود نداشتم، اگرچه در دانشگاه، دانشجو ناچار است تعدادی دروس علوم انسانی اخذ کند. من تمام تلاشم را می کردم که از یاد گرفتن هر چیز در این مورد و کار کردن روی آن دوری نمایم. بعد از آن، وقتی سنم بیشتر شد قدری سخت گیری من در این زمینه کاهش یافت و یاد گرفتم که در این مورد مطالعه کنم. اما راستش هنوز آدمی بیشتر یک بعدی هستم و در موارد دیگری غیر از این یک بعد (بعد علمی) چیز زیادی نمی دانم. هوش من محدود است و از آن در یک جهت خاص استفاده می کنم.
- تیراناسوروس در پنجره
وقتی پسر بچه بودم در خانه مان یک دایره المعارف بریتانیکا داشتیم و پدرم عادت داشت مرا روی پایش بنشاند و برایم از دایره المعارف بخواند. ما با هم درباره دایناسورها حرف می زدیم . شاید هم در مورد برونتوزوروس یا تیراناسوروس رِکس صحبت می کردیم، به عنوان مثال چنین می خواند: « این موجود 25 فوت قد دارد و عرض سر آن 6 فوت است » و همین جا صحبتش را قطع می کرد و می گفت «ببینم مفهوم آن چیست. یعنی اگر آن در همین حیاط روبروی ما می ایستاد، قدش آن قدر بلند بود که می توانست سرش را از پنجره داخل کند. اما نه کاملا، چون سر او کمی عریض تر از پنجره بود و پنجره را می شکست».
هر چیزی را که با هم می خواندیم، به بهترین نحوی که بتواند به ذهنیت ما نزدیک تر باشد تصور می کردیم. این کار باعث شد یاد بگیرم که عمل کنم و هر چیزی را که می خوانم سعی کنم مفهوم و معنای آن را بفهمم. (با خنده) من عادت داشتم دایره المعارف را وقتی یک پسر بچه بودم بخوانم و آن را تعبیر کنم، خیلی هیجان انگیز و جالب بود که تصور گردد حیواناتی با این ابعاد وجود دارند. من از این که یکی از آنها از پنجره داخل شود نمی ترسیدم اما فکر کردم خیلی خیلی جالب بود که همه آنها منقرض شدند و در آن زمان هیچ کس نمی دانست چرا.
ما در نیویورک زندگی می کردیم، و معمولا تابستان ها به کوه های کَتسکیل می رفتیم. کوه های کتسکیل جایی بود که مردم در تابستان به آن جا می رفتند. آنجا مردم زیادی بودند لیکن پدرها در طول هفته برای کار کردن به نیویورك باز می گشتند و فقط آخر هفته ها دوباره به کوه می رفتند. وقتی پدرم از نیویورك می آمد مرا به میان جنگل می برد و برای من از چیزهای مختلف و جالبی که لابهلای جنگل اتفاق می افتاد صحبت می کرد – که بعد برایتان تعریف می کنم – اما مادرهای دیگر که این رفتار پدرم را می دیدند قطعا فکر می کردند که این کار خیلی خوبست و پدرهای دیگر هم باید پسرهایشان را برای قدم زندن به جنگل ببرند. آنها روی این موضوع کار کردند ولی در ابتدا به نتیجهای نرسیدند. برای همین از پدر من خواستند که همهی بچه ها را با خودش به جنگل ببرد، اما او قبول نکرد زیرا او با من یک ارتباط بخصوصی داشت و ما با هم یک امر شخصی در بین داشتیم. بالاخره بقیه پدرها مجبور شدند بچه هایشان را از هفته آینده برای قدم زدن به جنگل ببرند. دوشنبهی بعد وقتی همهی [پدرها] به سر کار برگشتند، بچه ها داشتند در مزرعه بازی می کردند که یکی از بچه ها به من گفت این پرنده را ببین، آیا می دانی از چه نوعی است و من گفتم: « کوچکترین نظری راجع به نوع این پرنده ندارم ». او ادامه داد «یک پرنده آوازه خوان گلو قهوهای است. پدرت چیزی راجع به اون بهت نگفته؟ ». ولی اینطور نبود: پدرم به من مطالبی یاد داده بود. او در حالی که به پرنده نگاه می کرد گفت: « می دونی که این چه پرندهای است؟ یک پرندهی آواز خوان گلو قهوهایست؛ اما به پرتقالی به آن … می گویند، به ایتالیایی …، به چینی …، به ژاپنی …، و غیره. و حالا تو در هر زبانی که بخواهی اسم آن پرنده را می دانی اما مطلقا هیچ چیز در مورد این پرنده نمی دانی. تو فقط فهمیدی که آدم ها در مکانهای مختلف آن را چه نامیده اند». و سپس از من خواست که با هم به تماشای پرنده ها بنشینیم.
او به من یاد داده بود که به هر چیزی توجه کنم. یک روز وقتی که داشتم با قطار اسباب بازیم بازی می کردم، (از همان قطارهایی که بچه ها آن را روی ریل می کشند.) یادم می آید که داخل واگن یک توپ بود، وقتی که واگن را می کشیدم چیزی در مورد حرکت توپ فهمیدم، به پیش پدرم رفتم و به او گفتم: « نگاه کن بابا من یه چیزی رو فهمیدم. وقتی که واگنرا می کشم توپ به عقب واگن حرکت می کند و وقتی ناگهان آن را متوقف می کنم توپ به سمت جلو حرکت می کند.» از او پرسیدم که چرا این اتفاق می افتد او پاسخ داد که دلیلش را هیچکس نمی داند. و ادامه داد: « قانون کلی اینه که چیزهایی که در حال حرکت اند سعی می کنند به حرکت خودشان ادامه بدهند و چیزهایی که ساکن اند تمایل دارند که ساکن باقی بمانند مگر اینکه شما آنها را هل بدهید که این تمایل اینرسی نام دارد و هیچکس نمی داند که چرا وجود دارد ». حالا من به درك عمیقی رسیده بودم چون پدرم فقط یک اسم به من یاد نداد، او تفاوت بین دانستن اسم یک چیز و خود آن را می دانست. چیزی که من هم خیلی زود یاد گرفتم. پدرم ادامه داد: « اگر دقیق نگاه کنی می فهمی که این توپ نیست که به عقب واگن می رود بلکه این عقب واگن است که تو داری بر خلاف حرکت توپ می کشی. یعنی توپ می ایستد یا حتی به خاطر اصطکاك به جلو حرکت می کند و به عقب نمی رود ». من به طرف واگن کوچکم دویدم و دوباره توپ را روی واگن گذاشتم و آن را از زیرش کشیدم در حالی که از کنار به آن نگاه می کردم دیدم که پدرم درست گفته است. وقتی که واگن را به جلو می کشیدم توپ اصلا به عقب نمی رفت. توپ نسبت به واگن به عقب می رفت ولی نسبت به بیننده کمی به جلو می رفت و در واقع عقب واگن بود که به آن می رسید. با این روش بود که من توسط پدرم تعلیم دیدم، با این نوع مثالها و فقط با بحث های جالب و دوست داشتنی، بدون هرگونه فشار و اجباری من مورد آموزش پدرم قرار گرفتم.







 ر فیزیک هست. ایشون علیرغم زندگی مشقت باری که داشته تنها کسی هست که علاوهبر نوبل فیزیک(۱۹۰۳) برندهی نوبل شیمی(۱۹۱۱) هم شده!
ر فیزیک هست. ایشون علیرغم زندگی مشقت باری که داشته تنها کسی هست که علاوهبر نوبل فیزیک(۱۹۰۳) برندهی نوبل شیمی(۱۹۱۱) هم شده!