در شاخهی آنالیز حقیقی، انتگرال ریمانی مفهومی است که در آن به شکلی ارتباط بین یک تابع و مساحت زیر آن را در یک بازه مشخص میکند. انتگرال ریمانی کاربردهای فراوانی در علم دارد و البته دچار کاستیهایی نیز هست. به منظور رفع کاستیهای انتگرال ریمانی، ریاضیدانان در پی ابداع کردن نظریات انتگرال دیگری برآمدند. یکی از این نظریات، نظریه اندازه و انتگرال لبگ است.
انتگرال ریمانی:
در فضای اعداد حقیقی بازهای چون (a,b) را درنظر بگیرید. انتگرال ریمانی تابع f(x) برروی این بازه، معادل مساحت زیر نمودار تابع است.
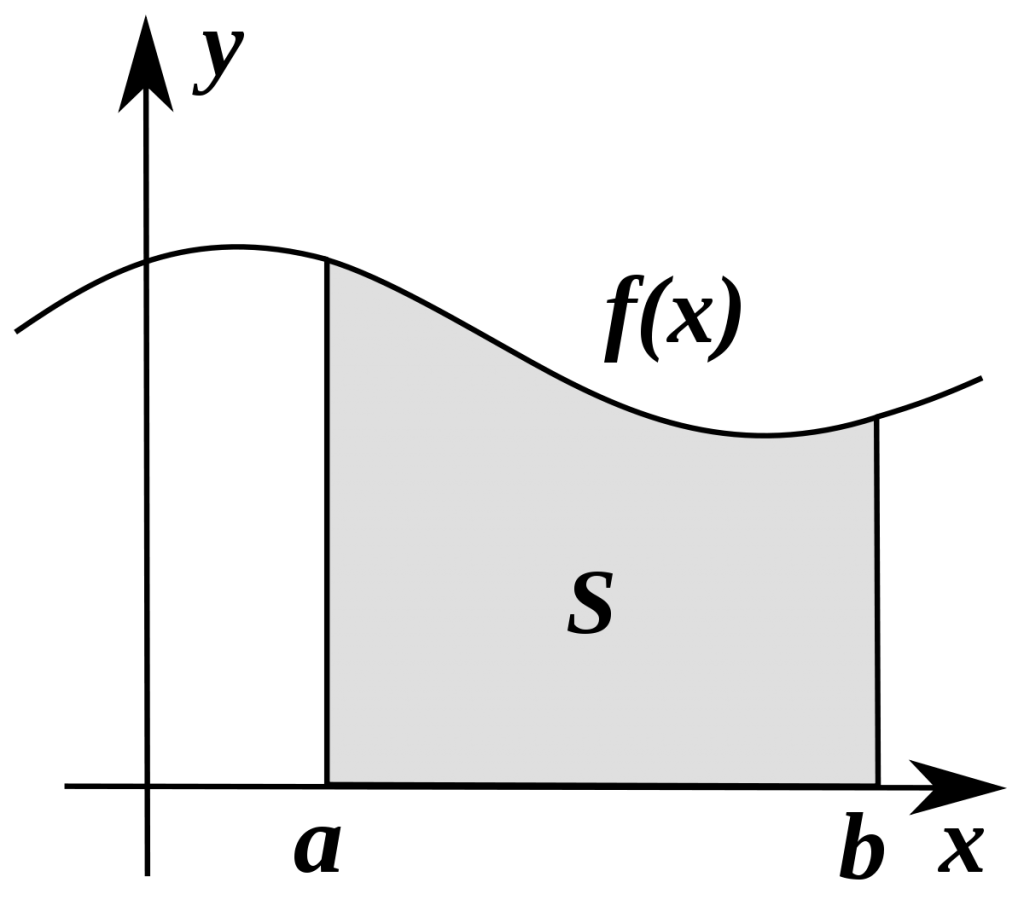
مقدار این انتگرال برابر است با:
$ S= \int_{a}^{b}f(x) dx $
ریمان برای محاسبهی مساحت زیر نمودار و معرفی انتگرال ریمانی، از ایدهی قسمتبندی کردن بازهای که انتگرال بر روی آن محاسبه میشود، استفاده کرد.به بیان ریمان اگر بازهها را به قسمتهای مساوی تقسیم کنیم بهگونهای که :$ a=x_{0} <x_{1} <… < x_{n} = b $ باشد و $ \Delta x_{i} = x_{i} – x_{i-1}$ . سپس با استفاده از دو مفهوم سوپریمم و اینفیمم (کوچکترین کران بالا و بزرگترین کران پایین) مجموعهای زیر را تعریف کرد.
$\sum_{i=1}^{n}M_{i} \Delta x_{i} = \sum_{i=1}^{n} \sup f(x) \Delta x_{i} $
$$ \sum_{i=1}^{n}m_{i} \Delta x_{i} = \sum_{i=1}^{n} \inf f(x) \Delta x_{i} $$
یک تابع انتگرالپذیر ریمانی است، هرگاه:
$$ \lim_{n\to\infty}\sum_{i=1}^{n} M_{i} \Delta x_{i} = \lim_{n\to\infty}\sum_{i=1}^{n} m_{i} \Delta x_{i} $$
هرگاه دو حد بالا موجود و برابر باشند، تابع انتگرالپذیر ریمانی است. انتگرال ریمان در شاخههای علم محاسبات را تسهیل کرده است، اما با نارساییهایی مواجه است که در ادامه به آن میپردازیم.
۱. انتگرال ریمان، یک انتگرال وابسته به وجود حد است.
به این معنی که برای وجود پاسخ انتگرال ریمانی باید دو حد $$ \lim_{n\to\infty}\sum_{i=1}^{n} \sup f(x) \Delta x_{i} $$ و $$ \lim_{n\to\infty}\sum_{i=1}^{n} \inf f(x) \Delta x_{i} $$ موجود باشد. در غیر این صورت، تابع انتگرالپذیر نیست.
۲. انتگرال ریمانی به پیوستگی تابع وابسته است.
توابعی که دچار ناپیوستگیهای اساسی باشند، انتگرالپذیر نیستند. (توابع تکهای پیوسته انتگرالپذیرند.)
۳.انتگرال ریمانی از R به R تعریف شده است.
یعنی اگر دامنه انتگرال به جای R ، $R^{2}$ باشد انتگرال ریمانی تعریف نشده است.
انتگرال لبگ و نظریهی اندازهها، کاستیهای انتگرال لبگ را رفع کرده است و کلاس خاصی از فضای هیلبرت را نیز ساخته است.
اندازه چیست؟
نظریه انتگرال لبگ نیازمند روشی ساختاریافته است که در آن بتواند مفهوم اندازه را معرفی کند. به بیان ساده اندازه تعمیمی از طول، مساحت، و حجم است. بازهی [a,b] را درنظر بگیرید. طول این باز معادل b-a است. حالا دو بازهی کاملا مستقل [a,b] و [c,d] را درنظر بگیرید. به نظر میرسد که طول مجموع این دو بازه (b-a)+(d-c) است. اگر بازهها زیرمجموعهی اعداد گنگ باشد چه میشود؟ آیا میتوان به سادگی مفهوم طول را معرفی کرد؟ به نظر میرسد اینجا نیازمند تعاریف دقیقتر ریاضی هستیم.
سیگما -جبر
مجموعهای به نام X را درنظر بگیرید. $ \Sigma $ یک مجموعه از زیرمجموعههای X است. آن را سیگما-جبر میگوییم، هرگاه ویژگیهای زیر را داشته باشد.
- X و تهی عضو سیگما باشند.
- اگر E عضو سیگما بود، متمم آن نیز عضو سیگما باشد.
- اجتماع تعداد شمارایی از اعضای سیگما، مجددا عضو سیگما باشند.
حال با دانستن تعریف سیگما- جبر به سراغ مفهوم اندازه میرویم؛
تابع اندازه ، $\mu (X)$،برروی مجموعهی X تعریف میشوند که X سیگما-جبر است. این تابع دارای خواص زیر است.
۱. اگر X مجموعه تهی یا تکعضوی باشد، اندازه آن صفر است. در غیر این صورت، اندازه آن همواره مثبت است.
۲.اندازهی مجموع دو مجموعهی بدون اشتراک برابر با مجموع اندازههای هرکدام از مجموعههاست. یعنی:
$$ \mu(X_{1} + X_{2})= \mu (X_{1}) + \mu(X_{2})$$
هرگاه
$$ X_{1} \cap X_{2} = \phi$$
اندازه لبگ
مهمترین قسمت انتگرالگیری لبگ، یافتن اندازه برروی مجموعهای است که روی آن انتگرال اعمال میشود. اگر یک مجموعه شامل ناپیوستگیهای بسیار باشد، باید راهی پیدا کنیم تا بتوانیم اندازه را بر روی این مجموعه تعریف کنیم. حاصل کار اندازهی لبگ است. با یک مثال ساده، انتگرال لبگ را تعریف میکنیم. بازهی بسته [a,b] به طول L را در نظر بگیرید. این بازه را میتوانیم به دو بازه با اشتراک صفر تقسیم کنیم. مجموعه X شامل نقاطی که عضو [a,b] هستند و ‘X (متمم مجموعهX) شامل نقاطی از [a,b] است که در X وجود ندارد. تصویر زیر را نگاه کنید.
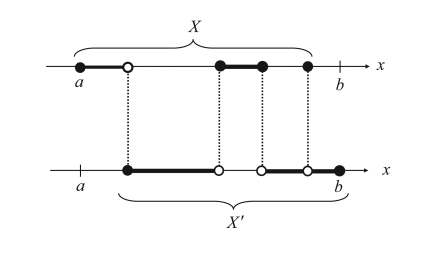
میخواهیم اندازه لبگ را بر روی این دو مجموعه تعریف کنیم. بدین منظور، X را با بازههای بدون اشتراک$\Lambda_{i}$نشان میدهیم. در بیان نظریه مجموعهها، داریم:
$$ \Lambda_{i} \subset [a,b]$$
$$\Lambda_{i} \cap \Lambda_{j} = \phi$$
$$X \subset (\Lambda_{1} + \Lambda_{2} +…)$$
اگر طول بازه $\Lambda_{k}$ را معادل $l_{k}$ بدانیم، از آنجا که طول بازه [a,b] برابر L است، نامساوی زیر صادق است.
$$ 0 \leqslant \Sigma_{k}l_{k} \leqslant L$$
کمترین مقدار $\Sigma_{k}l_{k}$ را اندازه بیرون مینامیم. به بیان دیگر :
$$ \mu_{out}(X) = inf (\Sigma_{k} l_{k} )$$
به همین ترتیب، مجموعههای $ \Lambda_{k}^{\prime} \subset [a,b]$ را معرفی میکنیم.
$$ X^{\prime} \subset (\Lambda_{1}^{\prime} +\Lambda_{2}^{\prime} +…) $$
$$ 0\leqslant \Sigma_{k} l_{k}^{\prime} \leqslant L$$
و اندازه داخل را به فرم $\mu_{in}(X)= L- \mu_{out}(X^{\prime}) = L- inf(\Sigma_{k} l{k}^{\prime})$ معرفی میکنیم. ضمنا
$$ 0 \leqslant \mu_{in}(X) \leqslant \mu_{out} (X) $$
زمانی $\mu_{in}(X) =\mu_{out}(X)$ شود، آنگاه $\mu_{in}(X)=\mu_{out}(X)=\mu(X)$ و $\mu(X)$ اندازه لبگ است.
انتگرال لبگ چیست؟
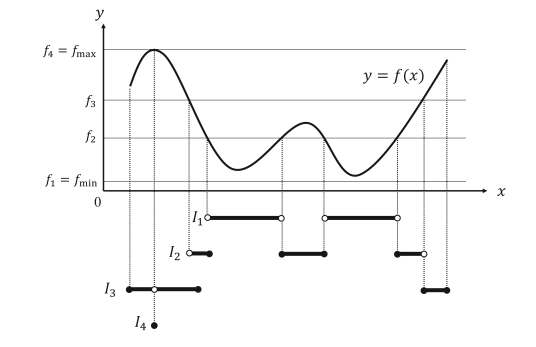
تابع f(x) را بهگونهای در نظر بگیرید که از بالا و پایین توسط بیشینه و کمینه خود محدود شده است.
$$ 0 \leqslant f_{min} \leqslant f(x) \leqslant f_{max}$$
تابع f(x) را به دنبالهی $ {f_{k}} $ تقسیم میکنیم به طوری که، $ f_{1}= f_{min}$ و $f_{n}=f_{max}$ باشد. با توجه به تناظر یک به یک بین x و f(x) مجموعههای $ X_{i}$ وجود دارند به گونهای که:
$$ f_{k} \leqslant f(x) \leqslant f_{k+1} , x \in X_{k} , 1 \leqslant k \leqslant n-1 $$
برای هر مجموعه $ X_{k} $، اندازهای درنظر میگیریم و اکنون میتوانیم مجموع لبگ را تعریف کنیم.
$$ \Sigma_{k=1}^{n} f_{k} \mu(X_{k}) $$
اگر در $ n\to \infty$ این مجموع همگرا شود، آنگاه میتوان انتگرال لبگ را تعریف کرد.
$$\int_{X} f d\mu \equiv lim_{max|f_{k}-f_{k-1}| \to 0} [\Sigma_{k=1}^{n} f_{k} \mu(X_{k})]$$
انتگرال ریمان و انتگرال لبگ
اکنون قصد دارم انتگرال ریمان را به روش انتگرال لبگ تعریف کنم تا بهتر متوجه شباهتها و تفاوتهای آنها شویم.
تابع f(x) که در بازهی [a,b] تعریف شده را در نظر بگیرید. اگر $X=[a,b]$ را به بازههای بدون اشتراک $X_{i}$ تقسیم کنیم، مجموع ریمان به فرم زیر تعریف میشود.
$$ \Sigma_{k=1}^{n} f(\xi_{k})\mu(X_{k}) , \xi_{k} \in X_{k}$$
این مجموع بهگونهای تعریف شده است که هر گاه $ n\to\infty$ برای هر $X_{k}$ ، $\mu(X_{k}) . . . \to 0$ در صورت وجود حد $\lim_{n \to \infty} \Sigma_{k=1}^{n} f(\xi_{k}) \mu(X_{k})$ این مجموع، انتگرال ریمان تابع f(x) بر X است.
اگرچه تعریف مجموع لبگ با مجموع ریمان که در بالا تعریف کردیم، شباهتهایی دارد،اما تفاوتهای اساسی در این دو مجموع مشهود است. در مجموع ریمان، f(x) را در هر نقطهی دلخواه $\xi_{i} \in X_{i}$ درنظر میگیریم. اما در مجموع لبگ مقدار f(x) را در هر زیرمجموعه $X_{k}$ درنظر میگیریم. به اینترتیب برای وجود انتگرال لبگ نیازی به شرط هموار بودن موضعی تابع نداریم. به دو شکل زیر نگاه کنید تا آنچه که اینجا بیان شده است، بهتر مشخص شود.
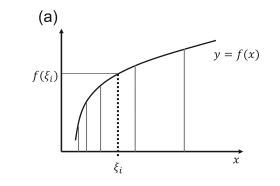
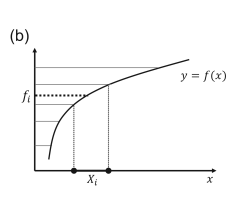
ویژگیهای انتگرال لبگ
۱. انتگرال لبگ یک تابع صفر است، هرگاه اندازهی مجموعهی آن صفر باشد.
۲. انتگرال لبگ یک تابع متناهی است، لذا زیرمجموعهی $X^{\prime}=\{x| f(x)= \pm\infty\}$ وجود دارد بهطوری که$\mu(X^{\prime})=0$ به بیان دیگر، زمانی که f(x) همگراست، الزاما اندازه مجموعههایی که در آن f(x) واگراست، صفر است.
۳.$\int_{X} f(x) d\mu$ متناهی است و $X^{\prime} \subset X$. اگر $ \mu(X^{\prime}) \to 0$، آنگاه $ \int_{X^{\prime}} f d\mu \to \infty $.
۴. زمانی که f(x) برروی X مقادیر مثبت و منفی را اختیار کند، انتگرال لبگ به صورت زیر تعریف میشود.
$$ \int_{X} f d\mu = \int_{X} f^{+} d\mu + \int_{X} f^{-} d\mu$$
$$\int_{X} |f| d\mu = \int_{X} f^{+} d\mu – \int_{X} f^{-} d\mu$$


برابری تقریبا همهجا
در قسمتهای قبل مشاهده کردیم زمانی که اندازهی مجموعهای صفر باشد، آنگاه آن مجموعه دخالتی در انتگرال لبگ ندارد. همین ویژگی منجر به مفهوم «برابری تقریبا همهجا» برای توابع اندازهپذیر شد. این ویژگی نقش بسیار مهمی در توسعه آنالیز تابعی دارد.
میگوییم دو تابع f(x) و g(x) که برروی مجموعه X تعریف شدهاند، تقریبا همهجا با هم برابرند، هرگاه:
$$\mu \{x \in X : f(x) \neq g(x)\}=0$$
فضای $L^{p}$
فضای $L^{p}$، فضایی است که توسط توابع مختلط f(x) ساخته میشود. در این فضا $|f|^{p}$ انتگرالپذیرلبگ است. اگر p=2 باشد، $L^{2}$ عضوی از فضاهای هیلبرت است. زمانی که $p \neq 2 $ باشد، فضای $L^{p}$ خاصیت ضرب داخلی خود را از دست میدهد، اما $L^{p}$ همچنان فضای کامل است.
منابعی برای یادگیری نظریه اندازه و انتگرال لبگ:
در دانشکدههای علوم ریاضی برای یادگیری این مباحث، عمدتا کتابهای قدیمی و معروف آنالیز حقیقی معرفی میشوند. از آنجا که من فکر میکنم با تغییر نسلها، منابع آموزشی نیز باید تغییر کنند کتابهایی را معرفی میکنم که اولا در دههی اخیر تالیف شدهاند. ثانیا، ادبیات و نحوهی روایت آن با ذهن کسانی که کمتر با ریاضیات مجرد آشنایی دارند، قرابت بیشتری دارد.
Functional anlysis for physics and engineering, Shima Hiroyuki 2016
A short course on the Lebesgue integral and measure theory, Steve Cheng
Elementary introduction to the lebesgue integral. Steve G.Krantz 2018