بهخاطر روایتگری در علم!
نویسنده: عباس ریزی
فیزیک آماری و علوم کامپیوتر:
سیستم‌های پیچیده، علم شبکه و پدیده‌های بحرانی
abbas.sitpor.org
برای بچه‌های دبیرستان (راهنمایی قدیم!) در مورد نظریه پیچیدگی صحبت کردم:
۱) اسلایدها:
سیستم‌های-پیچیده1۲) فایل صوتی:
۳) ویدیو:
قبل‌تر برای بچه‌های سال‌های اول، دوم و سوم لیسانس فیزیک، یک سری کتاب و کورس برای درس‌های مختلف معرفی کرده بودم. اما هیچ‌وقت در مورد ترمودینامیک و مکانیک آماری ننوشتم. راستش دلیل اصلیم هم این بود که هیچ کتابی رو پیدا نکردم که اکثر موضوعات رو به خوبی توضیح داده باشه و همین‌طور اون ایده‌های درخشان و جذاب ترمودینامیک رو هم به خوبی مطرح کرده باشه. از طرف دیگه، یه کتاب خوب از نظر من کتابیه که مسئله‌های چالش برانگیز و جدی هم داشته باشه. به همین خاطر همیشه از این‌که پیشنهادی در مورد ترمودینامیک یا مکانیک آماری داشته باشیم دوری کردم.
با این وجود، اکثر صاحب‌نظران معتقدند که ترمودینامیک و مکانیک آماری خیلی مهمه! خیلی! به قول ساسکیند تمام کله‌گنده‌های فیزیک، استادبزرگ فیزیک آماری بودند؛ از آینشتین گرفته تا فاینمن تا خود ساسکیند 🙂 ترمودینامیک پر از مفاهیم نابه که معمولا توی دوره لیسانس پشت حجم انبوه ابزارها مخفی میشه و دانشجوها اون درک لازم رو نمی‌تونند پیدا کنند. برای همین هم کاملا طبیعیه که بچه‌ها از این درس خوششون نیاد. تجربه شخصی خودم از روبه‌رو شدن با ترمودینامیک برای اولین مرتبه لااقل چیز خوبی نبود! بدون تعارف، دانشجوی فیزیک نیومده فقط یه مشت ابزار یادبگیره و سعی کنه مثل یک مهندس فکر کنه. شخصا متنفرم از این‌که درس ترمودینامیک در دانشکده فیزیک به همون شکلی ارائه بشه که در دانشکده شیمی یا مهندسی مواد ارائه میشه! چیزی که توی ترمودینامیک مهمه این نیست که یه ماشین گرمایی با فلان بازده طبق بهمان چرخه کار می‌کنه یا این‌که طی چه سازوکاری میشه فلان‌قدر گرما از این طرف اتاق به اون طرف اتاق منتقل کرد. یعنی این‌ها مهم هستند، ولی چیزهای بسیار مهم‌تری هم وجود داره. چیزهایی که ارزش ترمودینامیک رو به عنوان جامع‌ترین نظریه فیزیک مشخص می‌کنه. فراموش نکنید که ما برای یک پیستون گاز، یک غشا سلولی و یک سیاه‌چاله ترمودینامیک می‌نویسیم.
مفاهیمی مثل انتروپی و اطلاعات امروز معانی خیلی خیلی گسترده‌تری نسبت به قبل پیدا کردن. کلاس خوب ترمودینامیک کلاسی هست که شخص درک درستی از این مفاهیم پیدا کنه. معمولا توی کلاس‌های ترمودینامیک به سادگی از کنار پارادوکس‌های هیجان‌انگیز ترمودینامیک گذشته میشه، در صورتی که تمام بامزگی ماجرا همین پارادوکس‌ها و راه‌های برطرف کردنشونه.
با وجود همه چیزهایی که گفتم، به نظر من ترمودینامیک مهمه چون برای اولین بار دانشجوی فیزیک با یک «نظریه موثر» آشنا میشه و یاد میگیره که توی فیزیک میشه بدون این‌که جزئیات ریز سیستم رو دونست، در مورد مشاهده‌پذیرهای بزرگ‌مقیاس صحبت کرد. یادآوری کنم که توی ترمودینامیک یک گاز رو به عنوان یک سیستم در نظر می‌گیریم، به عنوان یک «کل» و با سه تا پارامتر دما، فشار و حجم در موردش صحبت می‌کنیم. به عبارت دیگه برامون مهم نیست که این گاز از چه اجزائی ساخته شده و این اجزا با همدیگه چه‌طور و با چه جزئیاتی برهمکنش می‌کنند. کل این سیستم بس‌ذره‌ای رو به کمک سه تا پارامتر که معمولا توسط یک قید مثل معادله حالت بهم وابسته شده توصیف می‌کنیم، نظریه هم به خوبی کار می‌کنه والسلام! به‌همین خاطر اگه فرد این نوع نگاه رو به ترمودینامیک بفهمه اون موقع انتظار می‌ره که درک کنه که چرا یک اقتصاد خرد داریم و یک اقتصاد کلان و ربطشون بهم چیه!
بعدها به‌طور مفصل در مورد مفهوم نظریه موثر خواهم نوشت، انشالله!فعلا این ویدیو رو ببینید! با این مقدمه بد نیست که یک سری پیشنهاد برای یادگیری ترمودینامیک و مکانیک آماری داشته باشیم. خوشحال میشم که تجربه‌های شما رو هم بدونم.
به نظرم اگر با مفاهیم پایه آشنایی دارید در حد چیزی که توی کتاب‌های فیزیک پایه در مورد ترمودینامیک نوشته شده اون موقع احتمالا روند زیر می‌تونه به درکتون از ترمودینامیک و مکانیک آماری کمک کنه. توی ویکی‌پدیا هم لیستی از کتاب‌های ترمودینامیک و مکانیک آماری وجود داره.
- عمیق بشید در کتاب Statistical and Thermal Physics: With Computer Applications نوشته Harvey Gould و Jan Tobochnik
- اگه کتاب بالا براتون سنگین بود کتاب گراینر رو بخونید همراهش!
- کورس ساسکیند هم که نمیشه معرفی نکرد! بهترینه برای شروع.
- برای حرفه‌ای شدن هم کورس مکانیک آماری مهران کاردر رو با حوصله دنبال کنید.
- برای بهتر شدن توی کارای محاسباتی هم کورس Statistical Mechanics: Algorithms and Computations رو شرکت کنید.
در کنفرانس سار، پاییز ۹۷ که ایده‌ش مشابه با کنفرانس‌های TEDx هست در مورد نظریه پیچیدگی حرف زدم. یک سخنرانی عمومی برای مردم!«داستان پیچیدگی: چرا بیشتر، متفاوت است؟»
🎞 دانلود ویدیو 🔊 دانلود صوت 🔖 اسلایدها 🎬 در آپارات
در همایش پیوند در تابستان گذشته در مورد این حرف زدم که چگونه ایده‌های برگرفته شده از فیزیک می‌تونن درک بهتری از شبکه‌های اجتماعی مثل فیس‌بوک به ما بدن. ویدیو این ارائه رو به همراه اسلایدها و فایل صوتی رو اینجا می‌ذاریم. ما بقیه ارائه‌ها رو هم در قسمت «سخنرانی‌ها، دوره‌های آموزشی و کلاس درس» می‌تونید پیدا کنید!
ویدیو:
سرطان به عنوان یکی از بیماری‌های که این روزها نامش بر سرزبان‌ها افتاده است، نامی است که به مجموعه‌ای از بیماری‌هایی اطلاق میشود که از تکثیر مهارنشده سلول‌ها پدید می‌آیند. سرطان عموما به عنوان بیماری ژن‌ها شناخته میشود؛ به این معنا که تغییرات ژنتیکی می‌توانند منجر به بروز این عارضه شود. از سوی دیگر، تلاش‌های صورت گرفته پیرامون کنترل و درمان سرطان عمدتا بر اساس شناخت ژن‌های موثر در سرطان‌های مختلف، تاکنون با چالش‌های زیادی همراه بوده است. در نگاه پیچیدگی، حرکت‌های جمعی برآمده از برهمکنش‌های یک سیستم بس‌ذره‌ای (سلول) تنها با مطالعه اجزای آن سیستم (ژن‌ها) قابل توصیف نیست و با دانستن این‌که هر جز (ژن) چگونه کار می‌کند، نمی‌توان درک کاملی از مقیاسی بزرگ‌تر (سلول) با سازمان‌دهی مرتبه-بالاتری پیدا کرد. در مورد ژن‌ها می‌دانیم که بیان هر ژن بر بیان سایر ژن‌ها اثر می‌گذارد و وجود این همبستگی‌ها سبب تشکیل یک حرکت جمعی میشود که خود باعث اثر گذاشتن روی بیان سایر ژن‌ها میشود. هدف این مطالعه، نگاهی پدیدارشناسانه به سرطان سینه و مقایسه رفتار جمعی ژن‌ها در نمونه سالم و سرطانی است. با در نظر گرفتن سلول به عنوان یک سیستم پیچیده، می‌خواهیم شبکه پیچیده‌ای که در پس این سیستم نشسته است را مورد مطالعه قرار دهیم به امید این که درک بهتری از سرطان از نگاه پیچیدگی پیدا کنیم.
بدین منظور، با در نظر گرفتن هر ژن به عنوان یک اسپین و برهمکنش ژن با ژن به عنوان ضریب جفت‌شدگی بین دو اسپین متناظر با آن‌ها در یک مدل شیشه-اسپینی (مدل گاوسی چند متغیره)، به دنبال استنباط این ضرایب هستیم. برای این کار با استفاده از اصل بیشینه آنتروپی، ماتریس برهمکنش را برای نمونه سالم و سرطانی یافته و از روی آن شبکه تنظیم ژن را برای دو نمونه بازسازی می‌کنیم. این شبکه‌ها، دارای یال‌هایی با وزن‌های مثبت و منفی هستند، بنابراین می‌توانیم در چارچوب نظریه توازن به این شبکه‌ها انرژی نسبت دهیم و تمایل شبکه‌ها نسبت به تغییر وضعیتشان را مورد بررسی قرار دهیم. نتایج ما نشان می‌دهد که توزیع مثلث‌های ایجاد شده در شبکه از یک الگوی توانی پیروی می‌کند. از نقطه نظر چشم‌انداز انرژی، انرژی شبکه سالم از شبکه سرطانی بیشتر است و این به معنای پویایی بیشتر سلول سالم نسبت به سرطانی است. شبکه سرطانی تمایل کمتری نسبت به تغییر وضعیت خود دارد و به همین خاطر دسترسی کمتری به وضعیت‌های قابل دسترس خود پیدا می‌کند. از سوی دیگر، در شبکه سرطانی، تعداد یال بیشتری دیده میشود. وجود یال بیشتر، به معنای ارتباط بیشتر بین اجزا و تاثیر بر دینامیک سلول است. رهیافت دنبال‌شده در این مطالعه به ما در یافتن درک بهتری از سلول به عنوان یک سیستم پیچیده کمک می‌کند.
| ارجاع به اثر: | arXiv:2010.05897 [q-bio.MN] |
2010.05897
تصمیم گرفتم تا جایی که می‌توانم، مسیر یادگیری سیستم‌های پیچیده را برای علاقمندانی که جرات یادگرفتن و شهامت حرکت کردن بیرون از مرزهای تعریف شده علوم را دارند را هموار کنم. برای شروع قصد دارم چند جلسه کلاس/سمینار در دانشگاه شهید بهشتی (تهران) برگزار کنم. ایده اصلی این جلسات لکچرهایی پیرامون مفاهیم اصلی سیستم‌های پیچیده است بیآنکه وارد جزئیات ریز آن شوم. می‌خواهم طی این جلسات افراد با پیش‌زمینه‌های مختلف با ایده‌های اصلی آشنا شوند.
فیزیک نیوتون و موضوعات مربوط به حساب دیفرانسیل و انتگرال که غالب تفکر علمی سه سده گذشته را تشکیل داده‌اند بر این ایده استوار هستند که هر چه مقیاس فضایی یا زمانی یک سیستم فیزیکی را ریزتر و ریزتر کنیم، با سیستمی ساده‌تر، هموارتر و با جزئیات کمتری روبه‌رو می‌شویم. ملاحظات دقیق‌تری نشان می‌دهد که ساختار ریزمقیاس سیارات، مواد و اتم‌ها بدون جزئیات نیست. با این وجود، برای بسیاری از مسائل، چنین جزئیاتی در مقیاس‌های بزرگ‌تر نامرتبط به حساب می‌آیند. از آن‌جا که این جزئیات مهم نیستند، فرموله کردن نظریه‌ها به شیوه‌ای که اصلا جزئیاتی وجود نداشته باشد منجر به همان نتایجی میشود که با در نظر گرفتن توصیف دقیقی از سیستم می‌توان به آن‌ها رسید.
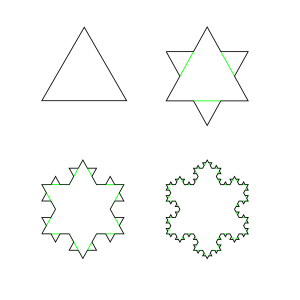
می‌دانیم در رویارویی با سیستم‌های پیچیده، هموار کردن پی‌در‌پی سیستم در مقیاس‌های ریزتر معمولا نقطه شروع مناسبی برای مطالعه سیستم به طور ریاضیاتی نیست. درک این موضوع، تغییر چشم‌گیری را در بنیادهای فکری ما به همراه داشته است.
در این سخنرانی ابتدا فرکتال‌ها، به عنوان موجوداتی که در مقیاس ریزتر جزئیاتشان را از دست نمی‌دهند را معرفی می‌کنیم. سپس بیآنکه سراغ جعبه ابزار نظریه میدان‌های کوانتومی رویم، ایده بازبهنجارش را به عنوان چارچوب جامع‌تری برای مطالعه رفتار سیستم‌ها در مقیاس‌های مختلف و چگونگی ارتباط این رفتارها مطرح می‌کنیم.