در پست قبل در مورد بالانس تئوری یا نظریه توازن صحبت کردیم و نشون دادیم که به کمک یک مدل ساده و ابتدایی می‌تونیم به جوامع، متناسب با نوع رابطه‌ی اعضا با همدیگه، انرژی نسبت بدیم و مقدار این انرژی به ما میگه که جامعه مد نظر در چه وضعیتی از توازن قرار داره.
بنابر بهنجارش، اگر انرژی جامعه ۱- به‌دست بیاد، جامعه کاملا متوازن یا بالانس هست که این در صورتی رخ میده که همه اعضای جامعه دوست همدیگه باشند و یا اینکه جامعه دو قطبی بشه، یعنی جامعه به دو زیر مجموعه تقسیم بشه به نحوی که درون زیرمجوعه‌ها اعضا دوست باشند اما هر عضوی از این زیرمجوعه با اعضای زیرمجوعه‌ی مقابل دشمن باشه. همین‌طور اگر انرژی جامعه بیشتر از ۱- به‌دست بیاد یعنی جامعه نامتوازن هست و هر چقدر که انرژی به ۱+ (کران بالای انرژی بنابر بهنجارش) نزدیک‌تر باشه جامعه نامتوازن‌تر هست که به معنی وجود امکان نزاع و درگیری در بین اعضاست.
طی این پست می‌خوایم ببینیم اگر به یک جامعه با شرایط اولیه مشخص (جمعیت و انرژی اولیه)، عضو جدیدی وارد بشه چه اتفاقی می‌افته. اما قبل از اون اجازه بدید که مدل باراباشی-آلبرت رو معرفی کنیم.
همه‌ی ما گزاره‌های این شکلی رو زیاد شنیدم: «پول، پول میاره» یا «ثروتنمندان، ثروتمندتر میشند و فقرا فقیرتر». بد نیست بدونید که جامعه‌شناسان به این پدیده می‌گند اثر متیو (Matthew Effect). ماجرا از اینجا شروع میشه که درون شبکه‌هایی مثل وب(www)، اینترنت، شبکه استناد (citation networks) و شبکه‌های اجتماعی اعضایی وجود دارند که علی‌رغم تعداد کمشون، توجه زیادی از شبکه رو به خودشون معطوف می‌کنند.
به عنوان مثال در بین تمام سایت‌ها گوگل، ویکی‌پدیا و فیس‌بوک بیشترین بازدیدکننده‌ها و پیوندها رو دارند یا مثلا در جامعه‌ی ما، محمدرضا شجریان، حسین علیزاده و کیهان کلهر جزو برجسته‌ترین هنرمندان موسیقی سنتی هستند، در مقایسه با جمعیت هنرمندان موسیقی، این افراد تعدادشون کمه. با این‌وجود شهرت و محبوبیشون از همه هنرمندان بیشتره. این شبکه‌ها، شبکه‌های بی‌مقیاس (scale-free) هستند به این معنی که توزیع درجه در این شبکه‌ها با تقریب خوبی از یک الگوی قانون‌توانی(power law) پیروی می‌کنه. این چندتا جمله‌ی سخت که گفتم یعنی اینکه وقتی ما این شبکه‌ها رو با یک گراف نمایش می‌دیم، درجه رئوس متناسب با وارون فراوانی(تعداد) اون رئوس هست . یعنی هرچی راسی درجه‌ش بیشتر باشه (تعداد یال‌های بیشتری بهش متصل بشند) فراوانیش کمتره و هر چقدر درجه راسی کم‌تر باشه فراوانیش بیشتره! همون‌جوری که تعداد سایت‌هایی مثل گوگل تعدادشون خیلی کمه، چون درجه‌شون زیاده.
کار آلبرت باراباشی و رکا آلبرت معرفی الگوریتمی بود که قادره چنین شبکه‌هایی رو مدل‌سازی کنه. این الگوریتم صرف‌نظر از تصادفی بودن باید گرافی رو تولید کنه که توزیع درجه رئوسش قانون‌توانی باشه. برای همین اساس این مدل دو چیزه:
۱) رشد: در طی زمان رئوس جدیدی به شبکه اضافه میشند.
۲) اتصال ترجیحی: رئوس جدید ترجیح می‌دند به رئوسی وصل بشند که درجه‌ی بالاتری دارند.
برای همین این الگوریتم ابتدا یک شبکه متصل (همبند) با 
راس ایجاد می‌کنه. بعد از اون، در هر مرحله، راسی اضافه میشه و به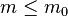 
راس قبلی وصل میشه. این m راس بر اساس درجه‌شون انتخاب میشند: یعنی احتمال اینکه راس جدید به iامین راس موجود درگراف وصل بشه برابره با نسبت درجه راس iام به مجموع درجات کل رئوس. این سبب میشه که «هاب» در شبکه به‌وجود بیاد. هاب‌ها رئوسی هستند که درجه شون از بقیه رئوس شبکه بیشتره. (صفحه شجریان در اینستاگرام یک هاب به حساب میاد در بین خواننده‌ها همون‌جوری که گوگل یک هابه در بین سایت‌ها!). يادتون باشه که در مدل باراباشی-آلبرت وزن هر یال ۱ است!
[…] منبع مطلب […]
سلام خدمت آقای کریمی
من بهمن هستم دانشجو برق قدرت میخواستم با شما همکاری کنم
سلام
لطفا مرام‌نامه رو بخونید.
سلام دوست عزیز،
از طریق سری مقالات فراکتال ها با این بلاگ آشنا شدم. واقعا از مطالبش لذت بردم. دست مریزاد
کار خوبتون رو ادامه بدید 😉
[…] با عنوان «برآمدگی اثر مقیاسی در شبکه‌های تصادفی» مدلی معروف به مدل شبکه «اتصال ترجیحی» رو منتشر کردن که نقش […]
[…] در نظریه گراف تلاش عمدتا بر شناسایی و مطالعه ساختارهاییه که بتونیم اون‌ها رو به صورت تحلیلی دنبال کنیم. برای همین، گراف‌کارها (نظریه‌پردازان گراف!) معمولا به سراغ گراف‌های تصادفی، گراف‌های کامل و مسائلی مثل رنگ آمیزی و کاور کردن میرن. اما در علم شبکه، مردم بیشتر به دنبال مسائل کاربردی‌تر و مدل‌هایی هستند که بیشتر مسائل دنیای واقعی (فیزیکی، شیمیایی، زیستی، اجتماعی و اقتصادی) رو توجیه کنند! برای همین لزوما از لحاظ ساختاری این شبکه‌ها، گراف‌هایی نه کاملا تصادفی و نه کامل، بلکه گراف‌هایی تنک با توزیع درجه‌‌های دم‌کلفت هستند! […]