نویسنده: امین هاشمی

رمزنگاری کوانتومی

منتشر شده توسط امین هاشمی در 12/07/2016

زندگی روزمره‌ی ما رو گستره‌ی وسیع و متنوعی از ارتباطات تشکیل میده. از یک عملیات ساده بانکی با کارت‌های اعتباری گرفته تا مکالمات تلفنی، ایمیل‌ها، نامه‌نگاری‌ها، فضاهای ابری و … که در هرکدوم از این‌ها کلی اطلاعات رد و بدل میشه. اما همواره مساله اساسی که وجود داره، خطر دزدیده شدن اطلاعات در این ارتباطاته و می‌دونیم هرچقدر ارزش اطلاعات بیشتر باشه خطر بزرگتری هم اونا رو تهدید میکنه.

میخوایم توجه خودمون رو معطوف این پرسش کنیم که آیا امکان برقراری ارتباط کاملا امن بدون ترس از دزدیده شدن اطلاعات وجود داره یا نه ؟

مساله‌ی تامین امنیت ارتباطات از گذشته‌های دور مورد توجه ویژه مردم بوده. مثلا در جنگ‌ها اطلاعات مهم و سری باید با حداکثر ایمنی جابجا میشد و این خودش یک مساله بزرگ به حساب میومد و بعضی وقتا بیسیم‌چی‌ها از کلمات رمزی برای این کار استفاده می‌کردند. با گذشت زمان ابزار رمزنگاری هم کم‌کم به دست بشر پیشرفت کرد و راه‌های زیادی طراحی و اجرا شد.

یکی از روش‌های کلاسیک رمزنگاری روش “ One-time Pad ” است. این روش امنیت نسبتا بالایی داره. فرض کنید با این روش یک متن رو رمزگذاری کردید. متن رمزگذاری شده‌ی شما هیچ اطلاعاتی از متن اصلی نداره و اگر کسی قصد دزدیدن اطلاعات رو داشته باشه، نمیتونه از متن رمزگذاری شده چیزی متوجه بشه. ویژگی مهم این روش اینه که برای رمز گذاری از کلیدی استفاده میشه که به اندازه متن طولانیه و کلیدمون یکبار مصرفه!

بیایم یک مثال برای این روش بزنیم. فرض کنید آلیس و باب میخوان یک پیام متنی برای هم بفرستن. مثلا آلیس میخواد کلمه “QUANTUM” رو برای باب بفرسته. در مرحله اول آلیس با توجه به جایگاه هر حرف یک عدد به اون نسبت میده:

message: Q U A N T U M

message: 17 (Q) 21 (U) 1 (A) 14 (N) 20 (T) 21 (U) 13 (M)

برای ساخت کلید آلیس از اعداد تصادفی استفاده میکنه و به هر عدد تصادفی میتونه یک حرف رو نسبت بده:

key: 24 (X) 22 (V) 2 (B) 10 (J) 3 (C) 8 (H) 12 (L)

تو این قسمت اعداد رو دو به دو باهم جمع میکنه:

message + key: 15 (O) 17 (Q) 3 (C) 24 (X) 23 (W) 3 (C) 25 (Y)

و در نهایت آلیس یک متن رمزگذاری شده (ciphertext) تولید کرده:

ciphertext: O Q C X W C Y

حالا کاری که باید باب انجام بده چیه؟ باب متن رمزنگاری شده رو از آلیس دریافت میکنه:

ciphertext: O Q C X W C Y

و اعداد مربوط به هر حرف رو هم میدونه:

ciphertext: 15 (O) 17 (Q) 3 (C) 24 (X) 23 (W) 3 (C) 25 (Y)

حالا اگه باب کلید رو در اختیار داشته باشه میتونه به راحتی (با یک تفریق ساده!) به متن اصلی دست پیدا کنه:

key: 24 (X) 22 (V) 2 (B) 10 (J) 3 (C) 8 (H) 12 (L)

ciphertext – key: 17 (Q) 21 (U) 1 (A) 14 (N) 20 (T) 21 (U) 13 (M)

message: Q U A N T U M

اما این روش رمزنگاری یک سری مشکلات رو هم به همراه داره. یک مشکل بزرگ اینه که اعداد تولید شده برای ساختن کلید، واقعا تصادفی نیستند. در واقع اعدادی که کامپیوتر به اسم اعداد تصادفی برای ما تولید میکنه، از الگوریتم‌های خاصی پیروی می‌کنند و اونجوری که باید، اعداد تصادفی نیستند. خب اگه سارقِ اطلاعات بتونه روند تولید عدد تصادفی رو حدس بزنه ، به راحتی به کلید دسترسی پیدا میکنه و میتونه بدون اینکه ما متوجه بشیم اطلاعات رو بدزده. یکی دیگه از مشکلات بزرگ این روش اینه که کلید تولید شده به اندازه متن طولانیه و یکبار مصرفه و اگر بخواهیم متن‌های زیادی رو رد و بدل کنیم، دفترچه‌ی چند صد برگی از کلیدها رو هم نیاز داریم که بنظر معقول نمیاد. اما مهم‌ترین مشکل در رد و بدل کردن کلید پیش میاد. کلید ساخته شده توسط آلیس چه‌جوری به دست باب باید برسه؟! از طریق خطوط ارتباطی مثل اینترنت یا تلفن؟ یا مثلا با یک پیک موتوری؟ می‌دونیم اگه کلید لو بره و دست سارق اطلاعات بیفته علاوه بر اینکه متن رمزگذاری شده رو میتونه بخونه، میتونه الگوریتم تولید کلید رو هم بدست بیاره و بقیه ماجرا. همه‌ی این‌ها باعث میشه به این نتیجه برسیم که ” One-time Pad ” روش ایده آلی برای رمز نگاری نیست.

اما یک روش کلاسیک رمز نگاری دیگه هم وجود داره که بر اساس الگوریتم‌های ریاضی بنا شده . اگه بخوایم بطور خیلی مختصر توضیح بدیم، تو این روش یک کلید عمومی وجود داره و از اون برای رمزگذاری استفاده میشه و کلید عمومی رو همه دارند. همچنین یک کلید خصوصی وجود داره برای گشودن رمز که این کلید فقط دست شخصیه که قراره اطلاعات رو به اون بفرستیم. این روش انوع مختلفی داره مثل Diffie-Hellman , RSA , Elliptic Curve . در واقع این روش بر اساس یک سری از توابع ریاضیاتی بنا شده که انجامشون از یک طرف آسون ولی باز گردوندنشون سخت و دشواره.

قبل اینکه وارد روش‌های رمزنگاری کوانتومی بشیم، یک سری از مفاهیم مکانیک کوانتومی رو باهم مرور می‌کنیم:

– میدونیم که هر حالت (state) کوانتومی رو میشه بر حسب بر هم نهی یک سری حالت پایه بنویسیم . حالا اگه بیایم روی اون اندازه‌گیری انجام بدیم، یک جواب یکتا بدست میاریم. مثلا اگر حالت مورد نظر از بر هم نهی ۲ حالت پایه ساخته شده باشه، همواره بعد از اندازه‌گیری یکی از حالت‌ها رو بدست میاریم و هیچوقت دوتاشون رو با هم در نتیجه‌ی آزمایشمون نداریم. (نگاه کنید به: Quantum superposition)

– اندازه‌گیری یک حالت باعث میشه سیستم در اون حالت اندازه‌گیری شده بمونه که اصطلاحا میگن سیستم به اون حالت فروریزش یا فروکاهش “collapse” کرده. (نگاه کنید به: Measurement in quantum mechanics)

– یک مفهوم دیگه هم در کوانتوم وجود داره که مفهوم درهم‌تنیدگیه ( “ entanglement” ) که میگه دو ذره (مثلا دو تا فوتون) که در هم تنیده شدن، با هم در ارتباطند، هر چند که از هم دور باشند و یجورایی همدیگه رو خبردار می‌کنند! مثلا اگه بیایم یکی از فوتون‌ها رو روش آزمایش انجام بدیم، این آزمایش رو اونیکی فوتون که ممکنه اونور دنیا هم باشه نتیجه مشخصی رو میده که از فیزیک کلاسیک زیاد قابل توجیه نیست!

– همچنین میدونیم فوتون یک بسته از نوره (اگه نور رو با دید ذره ای نگاه کنیم) .

– یک ویژگی که به فوتون‌ها میشه نسبت داد قطبیدگی یا قطبش اونهاست. (اگه بخواییم خیلی مختصر توضیح بدیم، قطبیده شدن یک فوتون یعنی اینکه اون‌ها رو از یک سری وسیله اپتیکی عبورشون بدیم تا بعد از عبور، در راستایی که ما میخواهیم حرکت کنند.)

– یک فوتون میتونه بصورت عمودی یا افقی قطبیده بشه و یا بصورت ترکیب خطی از قطبش عمودی و افقی وجود داشته باشه .

طبق نشان‌گذاری دیراک (Dirac notation) میتونیم حالت فوتونی که افقی(horizontally) قطبیده شده رو بصورت زیر تعریف کنیم:

$$ \left \vert \psi \right \rangle = \left \vert {H} \right \rangle $$

و همچنین فوتونی که بصورت عمودی(vertically) قطبیده شده رو میتونیم به این صورت نشون بدیم:

$$ \left \vert \psi \right \rangle = \left \vert {V} \right \rangle $$

همونطور که قبلا گفتیم فوتون ما می‌تونه به‌صورت بر هم نهی این دوحالت نیز وجود داشته باشه:

$$ \left \vert \psi \right \rangle = \alpha \left \vert {H} \right \rangle + \beta \left \vert {V} \right \rangle $$

حالا فرض کنید یک فوتون به ما دادن که در حالت زیره:

$$ \left \vert \psi \right \rangle = \alpha \left \vert {H} \right \rangle + \beta \left \vert {V} \right \rangle $$

ما میخوایم روی این فوتون آزمایش انجام بدیم و قطبیدگی اون رو اندازه بگیریم. بنظرتون نتیجه آزمایش چی میتونه باشه؟!

تجربه‌ی ما در آزمایشگاه نشون میده، دو جواب ممکنه برای این اندازه‌گیری بدست بیاد. یا به این نتیجه می‌رسیم که فوتونمون بصورت افقی قطبیده شده با احتمال:

$$ \left \vert \alpha \right \vert ^ 2 $$

و یا بصورت عمودی قطبیده شده با احتمال:

$$ \left \vert \beta \right \vert ^ 2 $$

و میدونیم همواره جمع احتمال‌ها برابر ۱ میشه، یعنی:

$$ \left \vert \alpha \right \vert ^ 2 + \left \vert \beta \right \vert ^ 2 = 1 $$

در مکانیک کوانتومی انتخاب پایه‌ها بصورت افقی و عمودی کاملا اختیاریه و شما میتونین برای توصیف پدیده‌ی کوانتومی مورد نظرتون (که در اینجا حالت فوتونمون بود) هر پایه ای که دوس داشته باشید انتخاب کنید (اگر کمی با جبر خطی آشنا باشید کاملا می‌فهمید که چرا میشه!) . برای ادامه بحث ما یک سری پایه جدید تعریف می‌کنیم و این پایه‌هامون نسبت به راستای افقی 45 درجه دوران دارند. یکی ازین پایه‌هامون قطریه(Diagonal) و به‌ این صورت:

$$ \left \vert {D} \right \rangle = \frac{1}{\sqrt{2}}(\left \vert {H} \right \rangle + \left \vert {V} \right \rangle )$$

و اونیکی پایمون هم پادقطریه (Anti Diagonal) و بصورت زیر:

$$ \left \vert {A} \right \rangle = \frac{1}{\sqrt{2}}(\left \vert {H} \right \rangle – \left \vert {V} \right \rangle )$$

حالا اگه دوباره قطبیدگی فوتونمون رو که این دفعه تو حالت قطریه اندازه گیری کنیم، چه نتیجه‌ای بدست میاریم!؟ در اینجا دو حالت به‌وجود میاد. حالت اول وقتیه که ابزاری که با اون اندازه‌گیری انجام میدیم، براساس پایه‌های قطری و پادقطری طراحی شده باشه. در اینصورت نتیجه اندازه‌گیریمون همواره (%۱۰۰) بصورت D بدست میاد. حالت دوم وقتیه که وسیله‌ی اندازه‌گیریمون بر اساس پایه‌های افقی و عمودی طراحی شده باشه. در این صورت ما هیچوقت یک جواب قطعی نداریم که بتونیم بگیم بعد از اندازه‌گیری چه نتیجه‌ای بدست میاریم یا به‌عبارت بهتر، هیچوقت به‌طور دقیق نمیتونیم بگیم سیستم بعد از اندازه‌گیری به کدوم یک از حالت‏‌های افقی یا عمودی “collapse” میکنه.

این یک موفقیت خیلی بزرگ به حساب میاد. چون کوانتوم مکانیک یک منبع طبیعی و بسیار قدرتمند برای تولید اعداد کاملا تصادفی در اختیار ما گذاشته . یعنی اگه روی فوتون قطریمون اندازه‌گیری انجام بدیم هر دفعه یک جواب بدست میاریم و در واقع در هر بار اندازه‌گیری به احتمال ۵۰ درصد جوابمون H و به احتمال ۵۰ درصد جوابمون V خواهد بود.

با در نظر گرفتن همه‌ی مفاهیم مطرح شده در مورد مکانیک کوانتومی تا اینجای کار، میریم سراغ اولین روش رمزنگاری کوانتومی با نام “BB84“. این روشِ ساختِ توزیعِ کلیدِ کوانتومی! (QKD) توسط “Gilles Brassard“ و“Charles Bennett“ در سال ۱۹۸۴ طراحی شد.

***در مورد پایه‌هایی که میتونیم در مکانیک کوانتومی برای فوتونمون انتخاب کنیم قبلا صحبت کردیم. حالا پایه‌هامون رو بصورت شماتیک، نمادگذاری میکنیم. پایه عمودی-افقی رو بصورت:

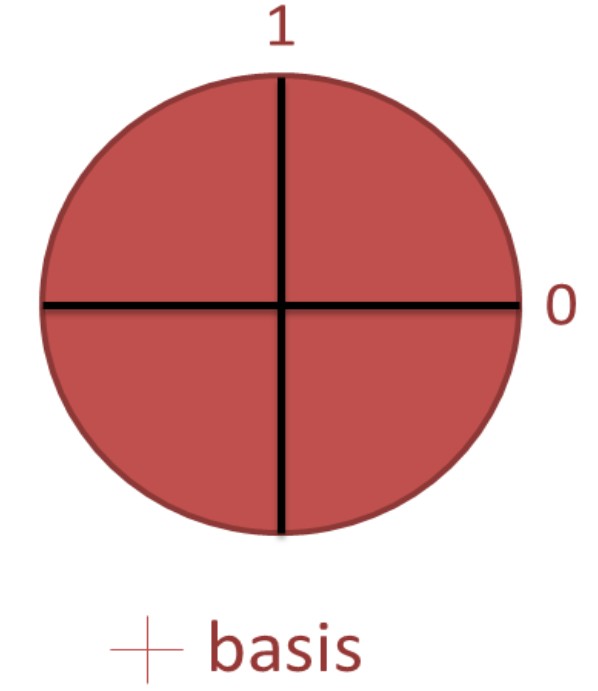
نشون میدیم که شامل یک حالت افقی 〈 H | (عدد 0 و نماد – ) و یک حالت عمودي 〈 V | (عدد 1 و نماد | ) میشه و همچنین پایه قطري-پاد قطري مورد نظرمون رو بصورت :

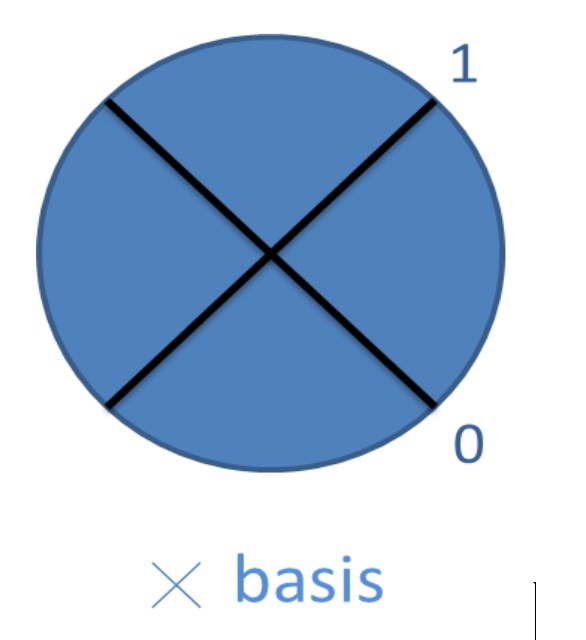
نشون میدیم که این پایمون هم یک حالت قطری 〈 D | (عدد 1 و نماد / ) داره و یک حالت پاد قطری 〈 A | (عدد 0 و نماد \ ).

باز هم میریم سراغ آلیس و باب به عنوان فرستنده و گیرنده اطلاعات. در مرحله اول، آلیس بصورت تصادفی یک سری پایه (Basis) برای خودش انتخاب میکنه. هدف آلیس اینه که یک رشته باینری شامل اعداد صفر و یک رو برای باب بفرسته. پس تو مرحله دوم باز هم بصورت تصادفی اعداد صفر و یک خودش رو تولید میکنه (Data). (قبلا گفتیم که مکانیک کوانتومی ابزار قدرتمندی برای تولید اعداد تصادفی دراختیارمون میذاره). در مرحله سوم آلیس از مقایسه پایه‌هایی که انتخاب کرده با اعدادی که تولید کرده، به یک سری از حالات (State) میرسه که این حالات میتونه افقی، عمودی، قطری و یا پاد قطری باشه (با توجه به توضیحاتی که در مورد پایه‌ها دادیم و قسمت ***).

در مرحله چهارم کار، باب هم به‌طور دلخواه و بصورت تصادفی، یک سری پایه برای خودش انتخاب میکنه. بدون اینکه از پایه‌هایی که آلیس انتخاب کرده با خبر باشه. حالا وقتشه که آلیس از طریق یک کانال کوانتومی حالت‌های (state) سیستمشو برای باب بفرسته. در عمل، این کانال کوانتومی، شامل همون فوتون‌های قطبیده شده میشه که از آلیس به سمت باب میره و این مرحله پنجم کار به حساب میاد. تو مرحله ششم ، باب با توجه به پایه‌ای که انتخاب کرده بود، حالتی (state) که آلیس براش فرستاده بود رو اندازه‌گیری میکنه. باز هم طبق اصولی که قبلا گفتیم دو حالت ممکنه به وجود بیاد. حالت اول وقتیه که آلیس و باب بطور تصادفی، پایه‌های یکسان انتخاب کرده باشند. در این صورت نتیجه اندازه‌گیری باب دقیقا همون حالتی میشه که آلیس براش فرستاده بود. اما حالت دوم وقتیه که پایه‌های آلیس و باب متفاوت بوده باشه. در اینصورت حالتی که باب بدست میاره با حالتی که آلیس براش فرستاده بوده متفاوته! (احتمالا باید بتونین حدس بزنین باب چه نتیجه‌های میتونه بدست بیاره!) باب بعد از اینکه همه حالاتی رو که آلیس فرستاده بود رو اندازه‌گیری کرد، تو مرحله هفتم، حالاتی که به‌دست آورده رو با پایه‌هایی که اول انتخاب کرده بود مقایسه میکنه و طبق قاعده‌ی قبلی به اون‌ها عدد نسبت میده. درنتیجه باب هم یک رشته از اعداد صفر و یک در اختیار داره .

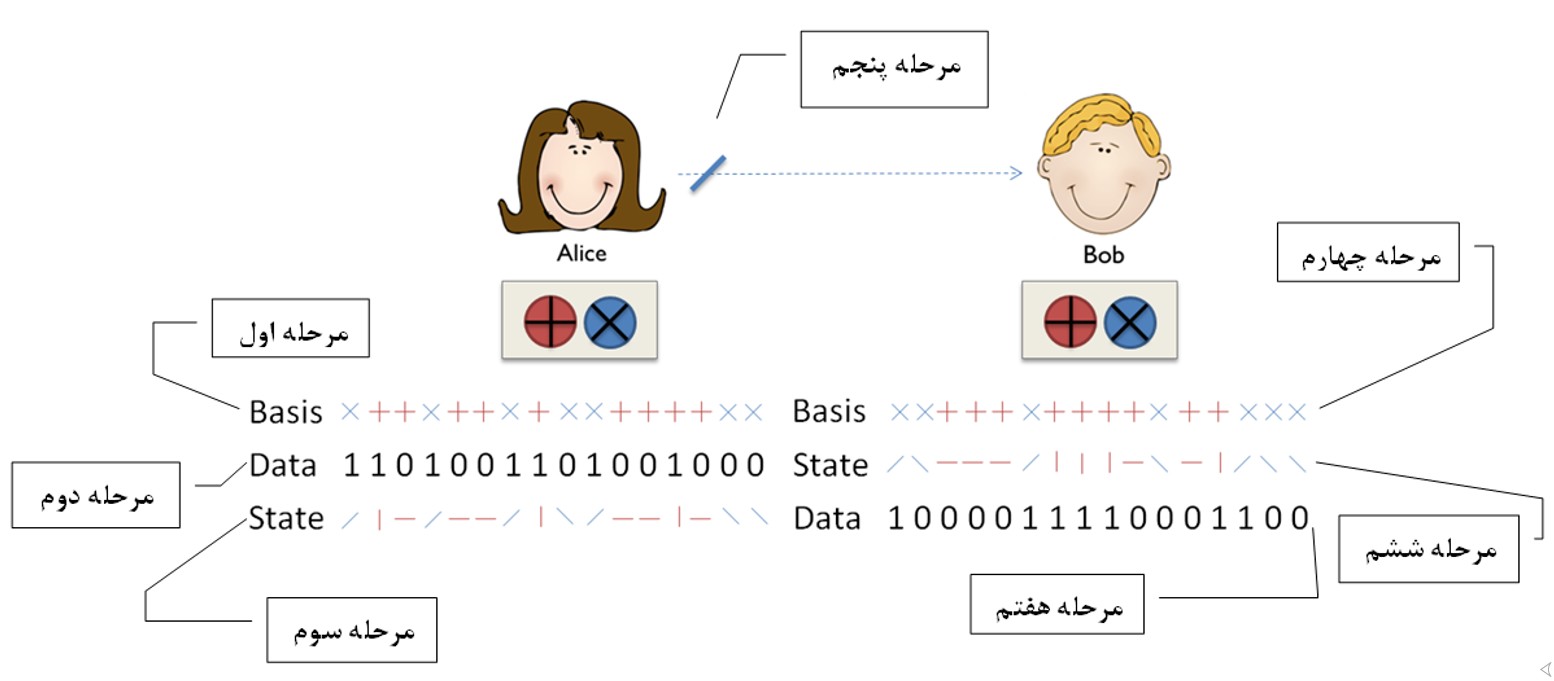
تا اینجا همه کاری که ما قصد داشتیم با مکانیک کوانتومی انجام بدیم تموم شدست. در مرحله هشتم ، آلیس و باب از طریق یک کانال کلاسیک، مثلا تلفن، با هم ارتباط برقرار میکنن و پایه‌هایی که انتخاب کرده بودند رو به هم اطلاع میدن. اگه پایه‌های انتخابی یکسان بود، اطلاعات مربوط به اون رو نگه میدارن و در غیر این صورت اون اطلاعات رو حذف میکنن.

چیزی که آلیس و باب در پایان کار در اختیار دارند، یک رشته از اعداد صفر و یک که برای جفتشون مشترکه و به این صورت آلیس و باب تونستند یک کلید بسیار ایمن برای رمزنگاری بسازند.

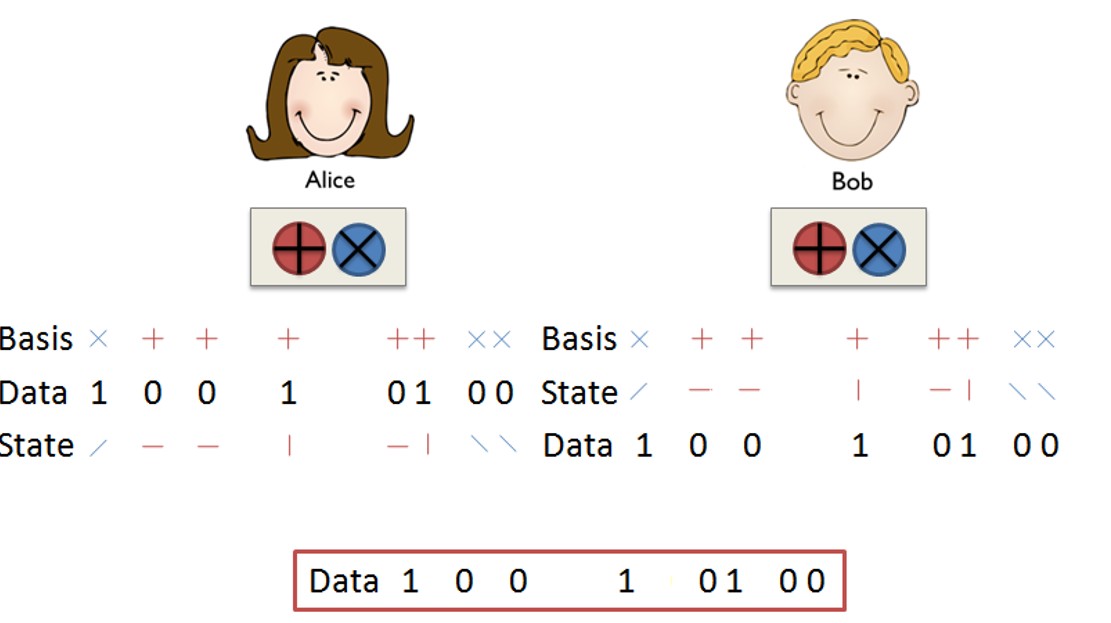
سوالی که اینجا مطرح میشه در مورد امنیت این روشه. اگه یکی این وسط بخواد اطلاعات رو بدزده چی؟ در این روش مهم ترین قسمت کار، انتقال حالت‌ها (state) از آلیس به بابه. چون در نهایت این قسمته کاره که باعث ساخت کلید ایمن میشه.خب اگه کسی بخواد تو این قسمت دزدی کنه، طبیعتا اول کار باید یک سری پایه برای خودش انتخاب کنه تا بتونه به وسیله اون‌ها روی حالت‌ها اندازه‌گیری انجام بده. اولین و بزرگترین مشکل برای سارق اینه که از پایه‌های باب هیچ اطلاعاتی نداره و به هیچ وجه نمیتونه پایه‌هاشو مثل باب انتخاب کنه. خب اگه بیاد در بین ارتباط آلیس و باب دزدی کنه، در پایان کار که آلیس و باب اطلاعات مربوطه رو رد و بدل کردن و کلید رو بدست آوردن، متوجه یک ناسازگاری بزرگ میشن. این ناسازگاری از اونجا ناشی میشه که اندازه گیری یک حالت کوانتومی باعث میشه سیستم در اون حالت بمونه و اصطلاحا سیستم به اون حالت فروزیزش یا فروکاهش “collapse” کنه. در اینجا هم دزد اطلاعات یک اندازه گیری انجام داده و حالتی که آلیس برای باب فرستاده بود رو عوض کرده و به این ترتیب آلیس و باب متوجه میشن که نفر سومی هم در ارتباط اون‌ها نقش داشته.

اما برای پیاده کردن این پروتکل چی نیاز داریم؟

در روش BB84 ، همه کار توسط فوتون‌ها انجام میشه. اما این فوتون‌ها باید “تک فوتون” (single photon) باشند و کوچکترین اختلالی در تولید فوتون که باعث بشه این ویژگی از بین بره، روند رمزنگاری رو با مشکل روبه‌رو میکنه. در عمل ساخت منابعی که برای ما تک‌فوتون تولید کنند بسیار سخت و بغرنجه!

پس برای این روش رمز نگاری ما به یک دستگاه تولید تک‌فوتون نیاز داریم. همچنین یک سری ابزار اپتیکی برای قطبیده کردن فوتون‌هامون. در نهایت، به دستگاهی برای آشکار سازی تک‌فوتون‌ها هم نیازمندیم.

برگردیم سراغ مکانیک کوانتومی؛ اگه به‌جای تک فوتونی که قبلا داشتیم، فرض کنیم دو تا فوتون در هم تنیده داریم، در واقع یک سیستم دو فوتونه که میتونیم بصورت زیر نمایشش بدیم (اندیس‌ها نشون دهنده‌ی شماره فوتون):

$$ \left \vert \psi \right \rangle = \alpha_{HH} ({\left \vert {H} \right \rangle_1}{\left \vert {H} \right \rangle_2}) + \alpha_{HV} ({\left \vert {H} \right \rangle_1}{\left \vert {V} \right \rangle_2}) + \alpha_{VH} ({\left \vert {V} \right \rangle_1}{\left \vert {H} \right \rangle_2}) + \alpha_{VV} ({\left \vert {V} \right \rangle_1}{\left \vert {V} \right \rangle_2})$$

برای سادگی کار سیستممون رو طوری تغییر میدیم که ۲ تا از جمله‌ها صفر بشند:

$$ \left \vert \psi \right \rangle = \alpha_{HH} ({\left \vert {H} \right \rangle_1}{\left \vert {H} \right \rangle_2}) + \alpha_{VV} ({\left \vert {V} \right \rangle_1}{\left \vert {V} \right \rangle_2})$$

حالا قطبیدگی فوتون اولمون رو اندازه‌گیری میکنیم. همون‌طور که قبلا گفتیم نتیجه میتونه عمودی یا افقی باشه. فرض کنید نتیجه اندازه‌گیری عمودی شد. اما سوالی که پیش میاد اینه که بعد از اندازه‌گیری سیستم به چه حالتی فروریزش (collapse) میکنه ؟ (دقت کنید که اندازه‌گیری فقط روی فوتون اول انجام شد)

نتایج اندازه‌گیری در آزمایشگاه بسیار شگفت‌انگیزه و به ما میگه پس از اندازه‌گیری سیستم به حالت زیر در میاد:

$$ \left \vert \psi \right \rangle = {\left \vert {H} \right \rangle_1}{\left \vert {H} \right \rangle_2}$$

و این نشون میده، اندازه‌گیری روی یک فوتون، روی فوتون دیگر هم تاثیر میذاره. حالا این دو فوتون درهم تنیده هر چقدر هم که میخوان از هم دور باشن، ولی باز روی هم تاثیر میذارن! نتیجه ای که از دیدگاه کلاسیک کاملا دور از انتظاره! دو فوتون در هم تنیده، باز هم ابزاری قدرتمندی در اختیار ما میذارن که با اون بتونیم عدد تصادفی تولید کنیم. چون اندازه گیری رو این فوتون ها دو نتیجه بیشتر نداره که احتمال اون‌ها کاملا با هم برابره.

بریم سراغ روش بعدی رمزنگاری کوانتومی یعنی روش “E91” که خیلی مختصر میخواهیم راجبش صحبت کنیم. این روش در سال ۱۹۹۱ توسط “ Artur Ekert “ مطرح شد؛ در این روش دو فوتون در هم تنیده داریم که آلیس و باب هرکدوم روی یکی از این فوتون‌ها آزمایش انجام میدن. باز هم مانند روش قبلی، آلیس و باب هرکدوم پایه‌های دلخواه خودشون رو به‌طور تصادفی، برای اندازه‌گیری انتخاب میکنن. چون فوتون‌ها در هم تنیده هستند و اندازه‌گیری روی هرکدوم ، وضعیت اون یکی رو هم مشخص می‌کنه، نتایج اندازه‌گیری الیس و باب به هم مربوط میشه و اگه از روش هایی مشابه به BB84 استفاده کنن، در نهایت یک کلید ایمن خواهند داشت. همچنین اگر کسی قصد دزدی اطلاعات رو هم داشته باشه، اختلال بوجود اومده در سیستم به راحتی برای آلیس و باب قابل مشاهده است. (جزئیات این روش نیازمند یک سری اطلاعات در مورد قضیه بل ، “Quantum teleportation” و چیز های دیگه میشه . برای همین به توضیح مختصر اون اکتفا کردیم.)

و در پایان مشاهده کردیم که چگونه مکانیک کوانتومی در برقراری ارتباط‌های ایمن به ما کمک میکنه و باعث میشه وجود هر اختلال حین برقراری ارتباط رو متوجه بشیم و بتونیم روشی برای انتقال ایمن اطلاعات داشته باشیم!

توجه:

استفاده از تصاویر و مطالب این پست، با ذکر منبع، بلامانع است.

چگونه‌ازكامپيوتردرفيزيک‌استفاده‌كنيم؟ حل عددی، قسمت دوم!

منتشر شده توسط امین هاشمی در 04/07/2015

در پست قبل از روش اویلر برای حل معادله دیفرانسیل مربوط به نیمه عمر رادیواکتیو استفاده کردیم. تو این پست هم میخوایم دوباره از این روش استفاده کنیم و یک حرکت پرتابی واقعی! رو شبیه سازی کنیم که کمی پیچیده تر از مثال مربوط به رادیواکتویه .

از معادله دیفرانسیل حرکت پرتابی شروع می کنیم. گفتیم که میخوایم حرکت پرتابیمون واقعی باشه، یعنی ما اثر مقاومت هوا رو هم روی جسممون در نظر می گیریم. اما حرکت ما در صفحه انجام میشه و باید معادلاتمون رو به دو راستا (x – y) تجزیه کنیم.

معادله دیفرانسیل های این حرکت بصورت زیر هستند (اگر با معادلات زیر مشکل دارید به کتاب‌های فیزیک پایه و یا مکانیک کلاسیک (تحلیلی) رجوع کنید) :

$$ \frac{\mathrm{d^2}{x} }{\mathrm{d} t^2}=\frac{F_{d,x}}{m} $$

$$ \frac{\mathrm{d^2}{y} }{\mathrm{d} t^2}=-g + \frac{F_{d,y}}{m} $$

که در این معادلات ${F_{d}}$ اثر مقاومت هواست و با سرعت حرکت جسم بصورت زیر رابطه داره :

$$F_{d}=-\beta v^2 \widehat{v}$$

همونطور که مشخصه معادله های دیفرانسیلمون مرتبه دو هستند. خب این کار مارو سخت نمیکنه، فقط کافیه هر کدوم از این معادلات رو به دو معادله مرتبه اول تبدیل کنیم. یعنی در پایان با چهار معادله دیفرانسیل مرتبه اول سر و کار داریم. حالا اگه ${F_{d}}$ رو هم به دو راستا تجزیه کنیم داریم:

$$F_{d,x} = F_{d} cos{\theta} = F_{d} \frac{v_{x}}{v} = -\beta v v_{x}$$

$$F_{d,y} = F_{d} sin{\theta} = F_{d} \frac{v_{y}}{v} = -\beta v v_{y}$$

و در نهایت چهار معادله دیفرانسیل مورد نظرمون به صورت زیر درمیاد :

$$\frac{\mathrm{{d} x} }{\mathrm{d} t} = v_{x} = f_{x}(t,x,v_{x})$$

$$\frac{\mathrm{{d} v_{x}} }{\mathrm{d} t} = -\frac{\beta}{m} v_{x} \sqrt{v_{x}^2 + v_{y}^2} = f_{vx}(t,x,v_{x})$$

$$\frac{\mathrm{{d} y} }{\mathrm{d} t} = v_{y} = f_{y}(t,x,v_{y})$$

$$\frac{\mathrm{{d} v_{y}} }{\mathrm{d} t} = – g – \frac{\beta}{m} v_{y}\sqrt{v_{x}^2 + v_{y}^2} = f_{vy}(t,x,v_{y})$$

حالا اگه از روش اویلر استفاده کنیم و این معادلات رو گسسته کنیم داریم :

$$x_{i+1} = x_{i} + \Delta t v_{x,i}$$

$$v_{x,i+1} = v_{x,i} – \Delta t \frac{F_{d,x}}{m}$$

$$y_{i+1} = y_{i} + \Delta t v_{y,i}$$

$$v_{y,i+1} = v_{y,i} – \Delta t (g + \frac{F_{d,y}}{m})$$

که در این معادلات t∆ گام گسسته‌سازی مساله ماست. حالا وقتشه که کد برنامه‌مون رو بنویسیم . کد این برنامه هم مثل برنامه رادیواکتیو خیلی سادست و نکته اضافی ای نسبت به اون نداره. دوباره به یک ساختار تکرار نیاز داریم که محاسبات رو تا زمانی که پرتابه مون به زمین نخورده( y >= 0 ) ادامه بده و به محض خوردن زمین عملیات رو متوقف کنه.

در ++c:

#include <iostream>
#include <fstream>
#include <math.h>
#define g 9.8
#define B 4e-5
#define m 1.0
using namespace std;
int main()
{
    double x, y, vx, vy, v, teta, t, dt = 0.1;
    /*** initial conditions***/
    t = 0;
    x = 0;
    y = 0;
    v = 100;
    teta = 30;
    vx = v * cos(teta * M_PI / 180);
    vy = v * sin(teta * M_PI / 180);
    /***-------------------***/
    ofstream o;
    o.open("Projectile motion.txt",ios::out);
    o<<"x"<<"\t"<<"y"<<"\t"<<"t"<<endl;
    while(y >= 0)
    {
        o<<x<<"\t"<<y<<"\t"<<t<<endl;
        v = sqrt(vx * vx + vy * vy);
        x = x + vx * dt;
        y = y + vy * dt;
        vx = vx - (B/m) * v * vx * dt;
        vy = vy - g * dt - (B/m) * v * vy * dt;
        t += dt;      
    }
    o.close();
}

در قسمت اول برنامه کتابخونه هایی که لازم داریم رو تعریف کردیم. کتابخونه math.h توابع مثلثاتی مثل sin و cos و همچنین یک سری از عملیات های ریاضی مثل جذر و یا به توان رسوندن رو شامل میشه (البته کلی توابع دیگه هم تو این کتابخونه هست!) و چون در بدنه برنامه نیاز به محاسبات ریاضی داشتیم از این کتابخونه استفاده شد. در خطوط بعد، ثوابت مورد نیاز در برنامه رو تعریف کردیم. همونطور که مشخصه در قسمت بعد و در بدنه اصلی برنامه، ابتدا شرایط اولیه رو که شامل مکان ابتدایی جسم، سرعت اولیه و زاویه پرتاب میشه تعریف و بعد سرعت رو به راستای افقی و عمودی تجزیه کردیم. در مرحله بعد فایلی برای ذخیره خروجی درست شد و بعد از اون الگوریتم اویلر برای حرکت پرتابی رو با استفاده از ساختار تکرار while پیاده کردیم.

و در پایتون:

from math import *
g = 9.8
m = 1.0
B = 4e-5
x = 0
y = 0
v = 100
teta = 30
t = 0
dt = 0.1
vx = v * cos(teta * pi / 180)
vy = v * sin(teta * pi / 180) 

f = open("Projectile motion.txt", "w")
f.write("x" + "\t" + "y" + "\t" + "t" + "\n") 
while y >= 0 :
    f.write(str(x)+"\t"+ str(y)+ "\t" + str(t) + "\n")
    v = sqrt(vx * vx + vy * vy)
    x = x + vx * dt
    y = y + vy * dt
    vx = vx - (B/m) * v * vx * dt
    vy = vy - g * dt - (B/m) * v * vy * dt
    t += dt

f.close()

قبل بررسی نمودار حرکت پرتابیمون بیاین پیش بینی کنیم که شکل حرکت چجوری میشه؟! خب در موقع بالا رفتن جسم، نیروی مقاوت هوا و نیروی وزن هر دو به سمت پایین هستن. اما در موقع برگشت، نیروی مقاومت هوا رو به بالا و نیروی وزن روبه پایینه و این یعنی برآیند نیرو های وارد به جسممون در رفت و برگشت فرق میکنه. حالا به نمودار زیر توجه کنین.

نمودار حرکت پرتابی در حضور و عدم حضور مقاومت هوا

همونطور که انتظار داشتیم، نمودارمون بطور کامل سهموی نیست و تقارن لازم رو نداره و این بخاطر وجود مقاومت هوا در برابر حرکت جسم ماست. مساله دیگه ای که وجود داره، برد پرتابه است. در حالت عادی و بدون مقاومت هوا میدونستیم که همیشه به ازای زاویه‌ی پرتاب 45 درجه برد پرتابه بیشینه میشه. اما با وجود مقاومت هوا دیگه اینطوری نیست.

برای تمرین بیشتر می تونین برنامه ی حرکت پرتابی رو طوری تغییر بدین که به ازای یک سرعت اولیه، برد بیشینه رو برامون پیدا کنه . همچنین میشه برای یک زاویه خاص، سرعتی که در اون زاویه برد بیشینه میشه رو بدست آورد.

در این پست هم یک معادله دیفرانسیل رو با روش اویلر حل کردیم. بازهم این پرسش مطرحه که همه ی معادله های دیفرانسیل با این روش حل میشه یا نه؟ و آیا روش های قدرتمند تر و مطمعن تری هم برای حل معادله دیفرانسیل وجود داره؟

به امید خدا پست بعد فضای متفاوت تری خواهد داشت ، اما در پست های بعدتر، باز هم به حل معادله دیفرانسیل و روش های مختلف برای حل این معادلات بر می گردیم.

چگونه‌ازكامپيوتردرفيزيک‌استفاده‌كنيم؟ این قسمت: حل عددی!

منتشر شده توسط امین هاشمی در 13/05/2015

سال‌ها بود که بشر به بسیاری از معادلات سخت ریاضی و ارتباط تنگاتنگشان با علومی مانند فیزیک رسیده بود. اما نکته‌ خیلی مهمی وجود داشت و آن انجام این محاسبات و کشف و بررسی پدیده‌های طبیعی مرتبط با آن‌ها بود. در بسیاری از موارد، انجام یک عملیات ساده ریاضیاتی ساعت‌ها و حتی روزها از دانشمندان وقت میگرفت و زمان مهمترین مساله به حساب می‌آ‌مد. انسان آن روزها به این فکر افتاد که چگونه می‌تواند این حجم وسیع از محاسبات را در زمان کمتر انجام دهد! و از همان روزها، اولین جرقه براي ساخت وسیله‌ای که بعدا به آن کامپیوتر گفتند زده شد. در سال 1937 میلادي اولین نسل از رایانه‌ها ساخته شد. البته قبل از این سال هم تلاش‌های موفقی در زمینه‌ی ساخت دستگاه‌های محاسباتی انجام شده بود. شاید کسی در آن زمان فکرش را نمی‌کرد رایانه‌ها تا حد امروزی بتوانند پیشرفت کنند. طوری که امروزه نمی‌توانیم نقش اساسی آن را در زندگی در نظر نگیریم. اما اگر از آن دوران بگذریم و برسیم به زمان خودمان، می‌بینیم به‌طور تخصصی در زمینه فیزیک، کامپیوترها نقش و جایگاه ویژه‌ای پیدا کرده‌اند که روز به روز در حال پررنگ‌تر شدن می‌باشد. شبیه سازی‌های گسترده‌ای که در فیزیک انجام میشود، محاسبات فیزیکی، طراحی آزمایشهای متنوع فیزیکی و . . . نمونه‌های کوچکی از کاربردهای کامپیوتر در فیزیک به حساب می‌آید.

رایانه کلوسوس به هدف شکستن کدهاي پنهانی آلمانیان در طول جنگ جهانی دوم ساخته شد

قصد دارم طی چند پست از کاربردهای مختلف کامپیوتر در فیزیک صحبت کنم و نمونه‌هایی از شبیه سازی‌ها، تحلیل داده‌ها و کمی هم پردازش تصویرهای انجام شده در فیزیک را مورد بررسی قرار دهم.

براي برنامه‌نویسی چه‌کار کنیم؟

خب با زبان‌های مختلفی می‌توانیم برنامه‌مان را بنویسیم. در اینجا براي نمونه از دو زبان برنامه نویسی استفاده میکنیم : ++C و Python و برنامه‌هایمان را با هر دو زبان می‌نویسیم. البته هرجا که نیاز باشد از نرم‌افزارهای دیگر هم حتما استفاده میکنیم تا با طیف گسترده‌تری از برنامه‌های کاربردی آشنا شویم. درواقع ++c که پیشرفته شده زبان c هست، یک زبان همه منظوره است که امکان برنامه نویسی شئ‌گرا جزو ویژگی‌های اصلی آن به حساب می‌آید و یک زبان برنامه نویسی با سطح میانی به حساب می‌آید. براي نوشتن کدها به زبان ++C میتوان از نرم افزار هاي مختلفی استفاده کرد. در سیستم عامل ویندوز نرم افزارهایی مثل ++Code Blocks، Dev C و Visual studio را شاید بتوان به عنوان ساده ترین و پرکاربردترین نرم‌افزارهای برنامه نویسی به زبان سی پلاس پلاس معرفی کرد. در توزیع‌های گنو/لینوکس به سادگی میتوان کدهای مورد نظر را در هر نرم‌افزار ویرایش‌گر متنی مانند gedit (در دسکتاپ گنوم) نوشت و در ترمینال اجرا کرد. (یا مثلا اینکه از نرم افزار geany استفاده کرد). اما در مورد پایتون باید گفت یکی از ساده ترین، پرکاربردترین و محبوب‌ترین زبان‌های برنامه‌نویسی به حساب می‌آید. دارای محیطی بسیار ساده و دلنشین است که ارتباط برقرار کردن با آن بسیار راحت می‌باشد. برای اطلاعات بیشتر به وب‌سایت پایتون رجوع بفرمایید.

برویم سراغ یکی از ساده‌ترین و تقریبا مهم‌ترین مباحث موجود در فیزیک: حل معادله دیفرانسیل. در بسیاری از مسائل فیزیکی(کلاسیک و غیرکلاسیک)، به یک معادله دیفرانسیل برخورد می‌کنیم. اگر سري به کتاب‌های آموزشی معادلات دیفرانسیل بزنید، راه‌های تحلیلی زیادی براي حل این معادلات پیدا خواهید کرد. از راه حل‌های ساده گرفته تا راه‌های پیچیده و دشوار. در اینجا می‌خواهیم به معرفی روش‌هایی که بتوان به‌سادگی بسیاری از معادلات دیفرانسیل را به صورت عددی (با کامپیوتر و برنامه نویسی) حل کرد، بپردازیم. در ضمن نکته بسیار مهمی که باید ذکر کنیم این است که بسیاری از معادله‌های دیفرانسیل جواب تحلیلی ندارند! و استفاده از روش‌های عددی تنها راه حل به حساب میآید.

روش حل عددی چیست!؟

در روش‌های عددی مساله را بجای اینکه پیوسته در نظر بگیریم(مانند حل تحلیلی)، گسسته فرض می‌کنیم سپس در بازه‌های زمانی کوچک جواب مساله را به دست می‌آوریم و مساله را با تقریب زدن ساده ترش می‌کنیم. اینکار را بارها تکرار میکنیم تا به جواب مورد نظرمان برسیم. براي انواع معادلات دیفرانسیل، انواع روش‌های عددی وجود دارد مثل : روش اویلر ، روش اویلر-کرامر، روش هون ، روش تیلور، روش رانگ-کوتا ، روش آدامز-بشفورت-مولتون و … .

با یک مثال ساده فیزیکی شروع کنیم:

می خواهیم نیمه عمر یک ماده رادیواکتیو را بررسی کنیم. نیمه عمر به مدت زمانی می‌گویند که ماده پرتوزا به نصف مقدار اولیه‌ی خود بر اثر واکنش‌های پرتوزایی تقلیل پیدا می‌کند. معادله دیفرانسیل مربوط به نیمه‌عمر رادیو اکتیو را میتوان بصورت زیر نوشت:

$$ \frac{\mathrm{d}N(t) }{\mathrm{d} t}=-\frac{N(t)}{\tau} $$

در این معادله ${N(t)}$ تعداد ذرات ماده برحسب زمان و τ طول عمر متوسط ماده‌ی پرتوزا است.${N(0)}$ مقدار اولیه ماده‌است و τ برای اورانیوم ۲۳۵ برابر با ۷۰۰میلیون سال است. حل تحلیلی این معادله به صورت زیر می‌باشد:

$$N(t)=N_0 e^{-t/\tau }$$

حالا میخواهیم این معادله را گسسته کنیم و در بازه‌های زمانی کوچک حلش کنیم و در نهایت حل عددی آن را با جواب تحلیلی مقایسه کنیم. ابتدا بسط تیلور تابع${N(t)}$ را می نویسیم:

$$N_{(t)}=N_0 +\frac{\mathrm{d}N_{(t)} }{\mathrm{d} t}\Delta t+ \frac{1}{2}\frac{\mathrm{d^2}N_{(t)} }{\mathrm{d} t^2}\Delta t^2+…$$

خب در بسط تیلور، هرچقدر t∆ کوچکتر باشد تقریب دقیق‌تری داریم (زیرا گسستگی کمتر میشود) و حتی می‌توانیم جملات از مرتبه 2 به بعد را هم نادیده بگیریم.زیرا هرچقدر t∆ کوچکتر باشد، در عمل وقتی به توان میرسد قابل چشم پوشی است. در نتیجه به معادله زیر میرسیم:

$$N_{(t)}\approx N_0 +\frac{\mathrm{d}N_{(t)} }{\mathrm{d} t}\Delta t $$ $$ \frac{N_{(t)}-N_0}{\Delta t}\approx \frac{\mathrm{d}N_{(t)} }{\mathrm{d} t}$$

$$\frac{\mathrm{d}N_{(t)} }{\mathrm{d} t}=\lim_{\Delta t\to 0}{\frac{N_{(t+\Delta t)}-N_{(t)}}{\Delta t}}$$

پس میتوانیم به راحتی نتیجه بگیریم :

$$N_{(t+\Delta t)}\approx
N_{(t)}+\frac{\mathrm{d}N_{(t)} }{\mathrm{d} t}{\Delta t}$$

این معادله در واقع مقدار تابع مورد نظر را در هر مرحله نسبت به مرحله قبل به ما میدهد (به اندیس ها توجه کنید).طبق معادله دیفرانسیل مربوط به نیمه عمر رادیواکتیو هم میدانیم${ \frac{\mathrm{d}N(t) }{\mathrm{d} t}=-\frac{N(t)}{\tau} }$ و در نهایت میرسیم به یک معادله تر و تمیز برای برنامه نویسی و محاسبه عددی:

$$N_{i+1}\approx
N_{i}-\frac{N_{i} }{\tau }{\Delta t}$$

به این روش گسسته‌سازی معادله دیفرانسیل، روش اویلرمی‌گویند.

خب تنها کاري که باید براي نوشتن برنامه انجام دهیم پیاده کردن الگوریتم اویلر است . خب اطلاعاتی که در اختیار داریم چیست؟ مقدار اولیه ماده (شرایط اولیه)، معادله دیفرانسیل مربوطه و گام گسسته‌سازی یا همان t∆ . کاري که باید بکنیم این است که${N_{i+1}}$ را نسبت به مرحله قبل حساب و مقدار آن را در هر مرحله ذخیره کنیم. پس در واقع ما به یک ساختار تکرار نیازمندیم که در هر مرحله زمان و ${N_{i+1}}$ را برایمان حساب و ذخیره کند. یک سری کارهای جانبی هم می‌ماند مثل تعریف متغیرها ، اضافه کردن کتابخانه ها‌ (در زبان ++c) و … که کارهای ساده‌ا‌ی هستند.

در ++c:

#include <iostream>
#include <fstream>
using namespace std; 
int main()
{
double N, dt = 0.01, T = 700, t = 0;
N = 100;
 ofstream o;
 o.open("Radioactive Decay.txt", ios::out);
 o<<"Time"<<"\t"<<"Numerical"<<endl;
 while(t <= 20)
 {
 o<<t<<"\t"<<N<<endl;
 N = N - (N / T) * dt;
 t = t + dt;
 }
 o.close();
}

و در پایتون:

t = 0
T = 700
N = 100 
dt = 0.01 
f = open("Radioactive Decay.txt", "w") 
f.write("Time" + "\t" + "Numerical" + "\n") 
while t <= 20 : 
‌               N = N - ( N / T ) * dt
               t = t + dt
               f.write(str(t) + "\t" + str(N) + "\n")
f.close()

سعی کردیم برنامه‌ها را در نهایت سادگی بنویسیم! در قسمت اول برنامه، متغیرهای مورد نیاز را تعریف کردیم و مقدارهاي اولیه را به آن‌ها نسبت دادیم. سپس یک فایل ایجاد کردیم تا اعداد محاسبه شده را در آن ذخیره کنیم. قسمت بعد با استفاده از یک دستور تکرار، الگوریتم اویلر را پیاده و اعداد را در فایلی که قبلا ایجاد کرده بودیم، ذخیره کردیم . حالا ما از این اعداد استفاده می‌کنیم و نمودارهاي مساله مورد نظرمان را رسم می‌کنیم.

در نمودارهای زیر حل تحلیلی و عددی را با هم مقایسه و درصد اختلاف آنها را با توجه گام گسسته‌سازی مقایسه کرده‌ام. به این نکته هم باید توجه کرد که شرایط اولیه مساله کاملا دلخواه است و می‌توان مساله را به ازای شرایط اولیه مختلف حل و جواب‌ها را مقایسه کرد.

نمودار 1 — حل عددی معادله دیفرانسل با ثابت زمانی 1 ثانیه و بازه های زمانی 0.05 ثانیه

حل تحلیلی معادله دیفرانسیل با ثابت زمانی 1 ثانیه

مقایسه حل تحلیلی و حل عددی با بازههای زمانی 1 ثانیه

مقایسه حل تحلیلی و حل عددی با بازههای زمانی 0.5 ثانیه

می‌بینیم که طبق انتظارمان حل تحلیلی و حل عددی بسیار به هم نزدیک هستند و با کاهش گام گسسته سازی جواب تحلیلی و عددی بسیار بهم نزدیک می‌شوند. معادله‌های دیفرانسیل زیادي را میتوان به همین سادگی حل کرد. می‌توان از بخش گرافیکی خود محیط برنامه‌نویسی هم استفاده کرد و نمودارها را در همان محیط برنامه‌نویسی رسم کرد (به زودی در مورد آن‌ها هم می‌نویسم). همچنین میتوان خروجی برنامه را برای تحلیل‌های دقیق‌تر و کارهای جالب و هیجان انگیز دیگر، به نرم‌افزارهای ریاضیاتی پیشرفته مثل Methematica داد.

چند سوال باقی می ماند: آیا همه معادلات دیفرانسیل را می‌توان با این روش حل کرد؟ اگر معادله دیفرانسیل مرتبه یک نباشد حل عددی آن چگونه می‌شود؟ حل‌های عددی برای هر مقدار اولیه و هر گام گسسته سازی دارای جواب قابل قبول هستند؟ به امید خدا در پستهای بعدي این سوالات را بررسی خواهیم کرد.

منابع
http://en.wikipedia.org/wiki/History_of_computing_hardware http://en.wikipedia.org/wiki/Python_(programming_language)
http://en.wikipedia.org/wiki/C%2B%2B Nicholas J Giordano_ Hisao Nakanishi-Computational physics-Pearson_Prentice Hall (2006)