در قسمت پیشین به تعریف فضا در مدل ولفرم پرداختیم و تکه آخر را که «زمان» باشد به این قسمت سپردیم. پازلی که پس از کامل شدن آن میتوانیم به مدلسازی نسبیت خاص در «فضا-زمان» برسیم.
جالب این جاست که مفهوم «زمان» در مدل ولفرم از دل یک «زیر قالی نکردن» پدیدار می شود. شاید این زیر قالی مأمن امنی برای تمام مسائلی باشد که ترجیح میدهیم به آنها فکر نکنیم. زیرا در رسیدن به مقصودمان مانع ایجاد میکنند اما این بار توجه ولفرم به یکی از آنها باعث شده است تا مفهوم زمان را از دل آن بیرون بکشد.
«ظهور مسئله» – نقطهای که علم از آن شروع میشود
شاید همهی ما در محیط آموزشی خودمان، شبیهسازی نرمافزاری کردهایم اما در حین این شبیهسازی با مسالهای مواجه شدهایم که آن را دانسته فرض کردهایم و یا خیلی راحت از کنار آن گذشتهایم. به گزاره و قانون پیشین یاد شده در قسمت قبل دوباره توجه کنید. قانون تحول سامانه به این شرح است که دو یال را انتخاب و حذف میکنیم و یک مجموعه یال جدید جایگزین آن میکنیم. اما کدام دو یال؟! در مجموعه حاضر انتخابهای زیادی داریم و با انتخاب و تحول آن در مرحله بعد به یک گراف متمایز میرسیم. پس کدام دو یال را باید انتخاب کنیم؟
به شکل آشنای زیر دقت کنید در ابتدا با همان شرط اولیه و قانون یاد شده در قسمت پیشین شروع میکنیم اما با انتخاب جفت یال متفاوت مسیر تحول ما تغییر میکند. درخت زیر نشان میدهد که اگر در هر مرحله جفت یال متفاوتی را انتخاب کنیم چگونه گراف حاصل از دیگر مسیرها متفاوت میشوند.

در چنین مواردی معمولا از این جزییات چشم پوشی میکنیم و بدون اثبات برای خود توجیه می سازیم که در بلند مدت این تفاوتها اهمیت پیدا نمیکنند اما چگونه و چرا این فرض را در شبیهسازی میکنیم. بیتردید پاسخ به آن دشوار است و ما تلاش میکنیم جزییاتی که نتیجهگیری دلخواهمان را به خطر میاندازند نبینیم!
شاید یکی از دلایل توجه نکردن به جزییات ظریف ما ریشه در «عجله برای نتیجه» داشته باشد. در دنیای آکادمیک امروز بسیار نتیجهگرا شدهایم. زیر بار فشار تمرین و مقاله که در مدت محدود باید تمام شوند؛ خیلی از این جزییات ظریف له می شوند. این بار کسی به این جزییات دقت کردهاست که سالهاست با دنیای آکادمیک صنعتی خداحافظی کرده است. یعنی ولفرم!
سخن نویسنده
«تلاش برای حل مسئله» – ذکاوت پژوهشگر
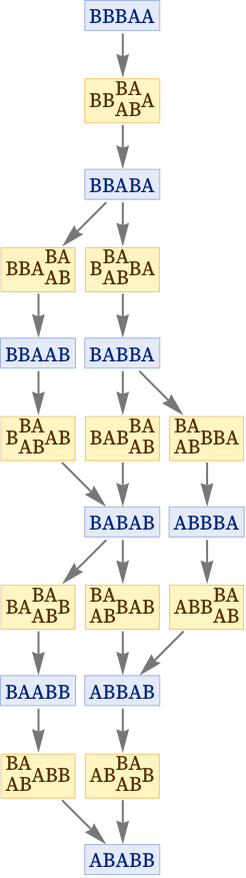
بیایید کمی این مسئله را بسط دهیم. ما یک شرایط اولیه داریم که به کمک یک قانون آن را متحول میکنیم. برای سادگی بیایید از تحول یک سامانه باهم حرف بزنیم که از حروف تشکیل شده است. با حالت BBBAA شروع میشود و قانون تحول آن به گونه زیر است.
شرط اولیه: BBBAA قانون تحول: $ { BA \rightarrow AB } $
همان طور که میبینید مسیرهای متفاوتی را میتوانیم برای تحول آن بپیماییم. سوال مهم اینجاست که اگر زمان را در مدل خود همگام با گامهای متحول سازی سامانه در نظر بگیریم دیگر خط زمانی واحدی نخواهیم داشت و در تعریف زمان دچار مشکل میشویم. اگر چه تمایل زیادی داریم تا «زمان» را معادل سلسله تحولات درون شبیهسازی خود بگیریم اما مشکل بوجود آمده نقد بزرگی به این معادلسازی وارد میکند.
اما زیرکی که ولفرم به خرج میدهد تا از پس این مشکل برآید ستودنی است. به مربعهای زرد رنگ درون شکل توجه کنید. این مربعها «رخدادهایی» را توصیف میکنند که طی آن حالت سامانه از یک مربع آبی به مربع آبی دیگر تغییر میکند. این رخدادها دارای خاصیت ترتیب هستند به این معنی که نوبت هر رخداد تنها زمانی فرا میرسد که رخداد قبلی آن اتفاق افتاده باشد. همچنین هر رخداد زمینه ساز رخدادهای بعد خود است. این ترتیب را با نام رابطه «علت و معلولی» میشناسیم. حال اگر هر علت را به معلولهای مستقیم آن متصل کنیم میتوانیم یک گراف جدید با نام «گراف روابط علّی» بسازیم.
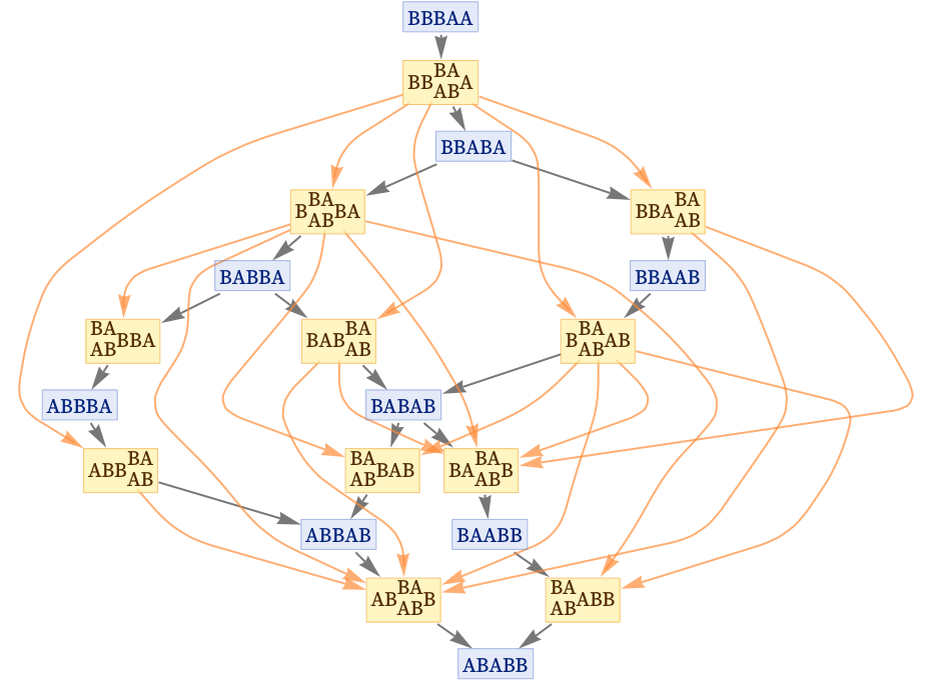
حال نشان میدهیم که چگونه گراف جدید میتواند مشکل بوجود آمده در توافق نداشتن خطوط زمانی بر سر تحول یکپارچه سامانه را حل و از میان بردارد. به شکل بالا مجددا دقت کنید. این درخت ۵ مسیر متفاوت را برای سیر تحول یک سامانه که با حالت مثالی BBBAA شروع میشود؛ توصیف میکند. اگر هر پنج مسیر را به صورت مجزا دنبال کنید و رخدادهای زرد رنگ و روابط آن را یادداشت کنید به پنج شکل زیر میرسید. هر کدام از این اشکال رخدادهای لازم برای تحول در یکی از این پنج مسیر را شرح میدهند.
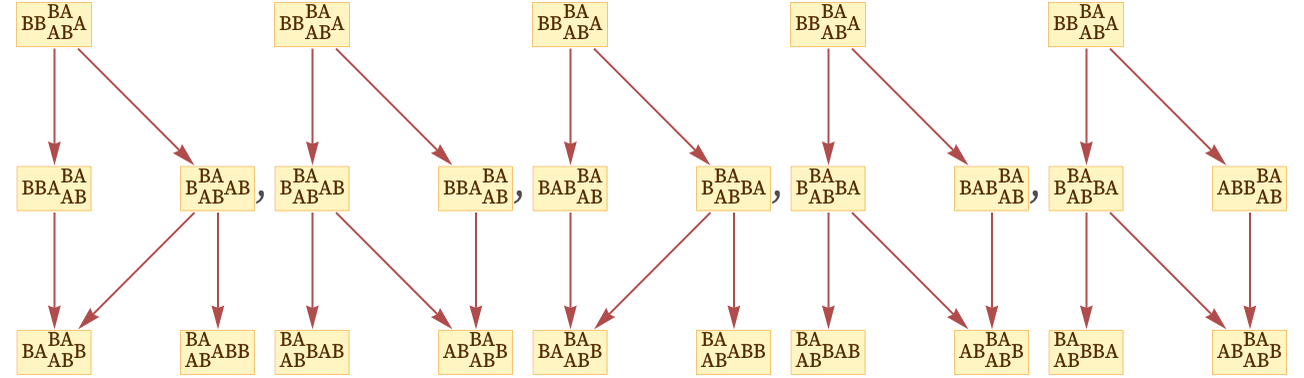
اگر به مجموعه پنجتایی بالا دقت کنیم؛ متوجه نکته ظریفی میشویم. هر پنج گراف جهتدار با هم «یکریخت» هستند. اگر چه برچسبهای هر نقطهی آنها باهم فرق دارد اما هر پنجتا یک نقطه دارند که دو یال خروجی و یک یال ورودی دارد که از سرچشمهای نشئت گرفته میشود که خود دو یال خروجی داده است. این به این معنی است که اگر چه مسیرهای متفاوتی را میتوان برای تحول این سامانه به صورت محاسباتی پیمود اما همهی آنها گراف علّی مشابه دارند.
به عبارت دیگر گراف علّی ما تحت مسیرهای متفاوت تحول «ناوردا» است. در واقع این خاصیت ناوردایی حاصل از نوع قانونی است که ما برای تحول انتخاب کرده ایم. قوانینی که این ناوردایی را در گراف علّی باعث میشوند، قوانین «casual invariance» یا «ناوردای عِلّی» میدانیم. این نوع از قانون، اختلاف بین تمام مسیرهای ممکن بین تحول گراف را به توافق میرساند و ما را در تعریف کردن مفهوم «زمان» یاری میکند.
حال که کلیدواژگان #رخداد، #علتومعلول و #ناوردایی را باهم دیدیم. کلیدواژه #نسبیت کمکم در ذهن ما به درستی تداعی میشود. جایی که دقیقا میخواهیم با زبان این مدل محاسباتی وارد آن شویم.
«نسبیت خاص» – یک اتفاق خوش!
بیاید با یک مثال ساده شروع کنیم. فرض کنید مانند قبل قرار است با یک قانون ساده، سامانه خود را متحول کنیم. یک رشته کاملا نامرتب مانند زیر درنظر بگیرید که قرار است آن را مرتب کنیم. قانون تحول آن هم به این گونه $BA \rightarrow AB$ است. این یک رشته کاملا بهم ریخته است به همین دلیل رخدادها در تکتک نقاط آن اتفاق میافتند. استفاده از این مثال به ما این امکان را میدهد تا رخدادها را در تمام نقاط «فضا» ببینیم.

شرط اولیه: BABABABABABABABABABA قانون تحول: $ { BA \rightarrow AB } $
فرض کنید میخواهید قصهی تحول این سامانه را برای یک شنونده روایت کنید. تا زمانی که شما ترتیب رخدادها را رعایت کرده باشید؛ بیتردید او به قصهی شما گوش خواهد کرد و اعتراض نخواهد کرد . به این معنی که اگر ابتدا یک معلول را روایت کنید و سپس علت آن را؛ او گیج خواهد شد و روابط علّی را گم خواهد کرد.
یک روایت مثالی میتواند چنین باشد که از بالای گراف روابط علّی شروع میکنیم و به سمت پایین به ترتیب حرکت میکنیم. هر تعداد رخداد که میتوانیم با رعایت ترتیب علت و معلول برای او همزمان بخوانیم را روایت کنیم. در شکل زیر، هر خط قرمز به ما نشان میدهد که در هر مرحله کدام رخدادها را برای شنونده بخوانیم.
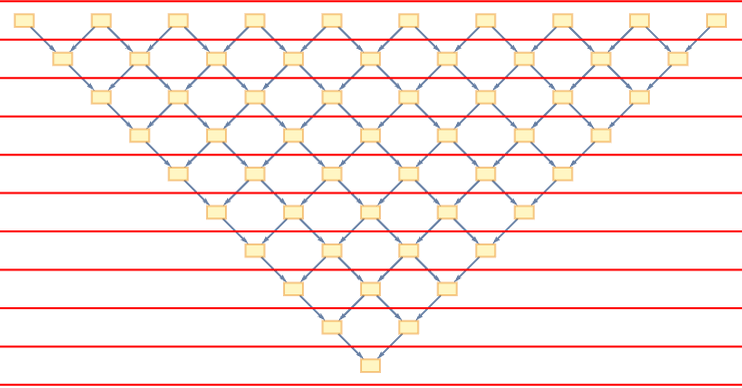
حال فرض کنید که شنوندهی دیگری داشته باشید که با سرعت ثابت حرکت کند. حرکت او باعث میشود تا قصهای را که تعریف میکنید متفاوت از شنونده اول بشنود. هر چه رخدادی در فاصله ی دورتری از او باشد با تاخیر بیشتری به دست او خواهد رسید. همین نکته باعث می شود رخدادهایی را که پیش از این شنوندهی اول همزمان دریافت میکرد، دیگر همزمان دریافت نکند. در واقع خطوط «همزمانی» مشابه شکل تغییر کرده است.
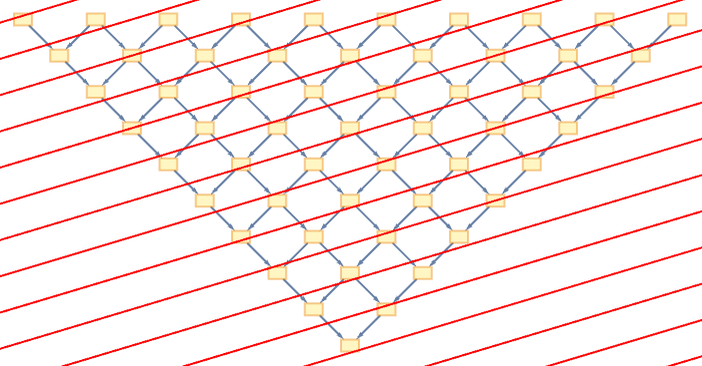
حرکت با سرعت ثابت نسبی است یا ما به دور جهان میگردیم یا جهان به دور ما!
در شکل بالا خطوط همزمانی را برای شنونده دوم رسم کردیم. اما شنوندهی دوم میتواند این طور فکر کند که این جهان است که به زیر پای او کشیده است و خودش ساکن بوده. او خود را شنوندهای مانند شنوندهی اول فرض میکند. پس میتوانیم از او بخواهیم که برای ما داستانی را که شنیده است برایمان مجددا تعریف کند!
حال بیاید روایت او را از قصهای که شنیده است بازسازی کنیم. برای این کار نیاز به یک تبدیل هندسی داریم. تبدیل هندسیای که تمام فضای موجود در شکل بالا را به گونهای تبدیل کند که خطوط مورب همزمانی شنونده دوم به حالت افقی درآیند. همچنین ترتیب روابط علی در گراف ما حفظ شود. آن تبدیل با دو شرط یاد شده، به صورت یکتا به قرار زیر درمیآید:
$ (t, x) \rightarrow (\frac{t – \beta x}{\sqrt{1-\beta^2}}, \frac{x – \beta t}{\sqrt{1-\beta^2}}) $
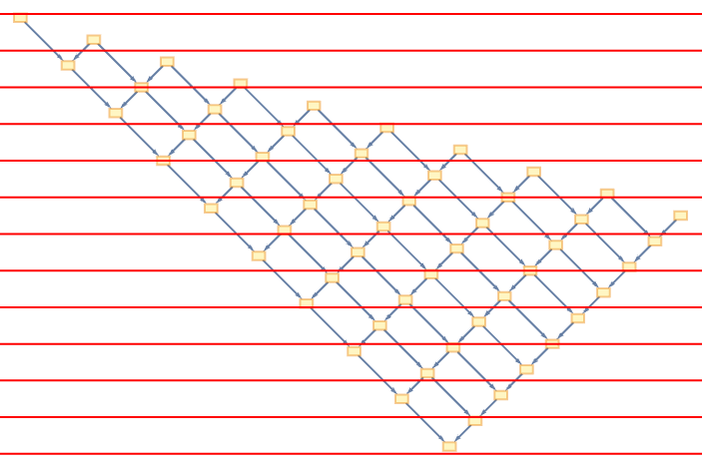
تبدیل یاد شده را با نام تبدیلات لورنتس میشناسیم. این تبدیلات به ما کمک میکنند تا دو روایت دو شنونده در حال حرکت را به یکدیگر تبدیل کنیم. همان طور که در شکل ۸ میبینیم شنوندهی دوم رخدادهای سمت چپ رشته حروف را زودتر از سمت راست میشنود. زیرا شنونده در حال حرکت است و خبر رخدادهای سمت راست زمان بیشتری را برای رسیدن به شنونده نیاز دارند.

حال که روایت شنوندهی دوم را بازسازی کردیم میتوانیم گراف علّی بدست آمده در شکل ۸ را روی صفحهی رخدادها بنشانیم و به ترتیب بخوانیم که شنوندهی دوم چگونه تحول سامانه را شنیدهاست.شکل ۹
همان طور که میبینید اگر چه شنیدن رخدادها کمی دیر و زود شده است اما هر دو شنونده در نهایت یک تغییر را برای رشته خواهند شنید. رشته حروف برای هر دو به حالت …AAABBB… خواهد رسید. این نتیجه میتواند با یکی از اصول نسبیت خاص انشتین معادل سازی شود. او در یکی از اصول خود ناوردایی «فیزیک» را در چارچوبهای ناظرهای مختلف اشاره کرده بود.
همچنین قابل توجه است که میتوانیم «اتساع زمانی» را توسط این مدل توضیح دهیم. دو رخداد از دو ردیف متوالی از شکل ۷ را در نظر بگیرید. در روایت دوم در شکل ۸ فاصلهی دو ردیف کمی کش آماده است. به این معنی که شنوندهی دوم فاصلهی زمانی بین آن دو رخداد را طولانیتر رصد میکند.
به این ترتیب به کمک مدل ولفرم توانستیم یکبار دیگر نسبیت خاص ونتایج آن را از نو بدست آوریم. قابل تقدیر است که این مدل در ادامه فراتر میرود و حتی به دنیای گرانش و کوانتوم مکانیک نیز پا میگذارد. برای مطالعه بیشتر در مورد این مدل میتوانید به صفحهی پروژهی فیزیک ولفرم پا بگذارید. او یک کتاب الکترونیکی مصوّر را برای شرح تمامی جنبههای مدل خود نوشته است.
در پایان با ذکر نکتهای کوتاه به این دو قسمت پایان میدهم. شاید در حین نوشتن این مقاله بسیار به نام ولفرم اشاره کردم و تصور میکنم که ناخودآگاه از او بتی را وصف کردهام. اما باید اینجا اشاره کنم که ولفرم نام یک گروه است و تمام این پژوهشها برآمده از یک تلاش گروهی بوده است کاری که امروزه در محیط دانشگاهی خودمان کمتر به آن پرداختهایم.