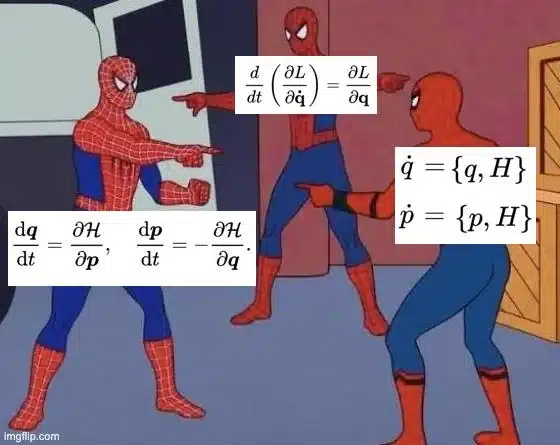
این میم بهونه خوبیه که در مورد روشهای متفاوتی که میشه مکانیک کلاسیک رو ارائه کرد حرف زد. پس توی این نوشته، بدون پرداختن به مکانیک کوانتومی، سراغ فرمول بندیهای مدرنی میریم که برای توصیف حرکت داریم.
صورتبندی نیوتون
نخستین فرمول بندی همانچیزی است که همه ما در مدرسه با آن آشنا شدهایم؛ صورتبندی نیوتون. نیوتون با ارائه سه قانون، چارچوبی کلی برای مطالعه حرکت معرفی کرد. با پذیرفتن این سه قانون، میشود حرکت ذرات غبار در هوا یا حرکت سیارات و کهکشانها را با دقت خوبی توضیح داد و پیش بینی کرد. به طور خلاصه به کمک قوانین نیوتون میتوانیم بگوییم زمین چگونه به دور خورشید میچرخد و اگر توپی را با فلان سرعت پرتاپ کنیم، کی به کجا میرسد.
قانون اول نیوتون در مورد ناظر است. این قانون میگوید برای داشتن درک درستی از حرکت اجسام، کسی که آنها را مشاهده میکند هم مهم است. در واقع نیوتون قوانین حرکتش را برای ناظرهایی ارائه میدهد که در ابتدای امر تکلیف آنها را مشخص کرده: ناظرهای لَخت. تعریف ساده ناظر لخت این گونه است: اگر جسمی را منزوی کنیم جوری که هیچ جسم دیگری روی آن اثری نگذارد، آن موقع، ناظر مورد نظر ما آنی است که ببیند جسم با سرعت ثابتی حرکت میکند. قاعدتا سرعت صفر(بیحرکتی) هم شامل این مورد میشود. بعد از مرور قانون دوم دوباره به این قانون فکر کنید. قانون اول از قانون دوم نتیجه نمیشود!
به دنبال قانون اول، قانون دوم نیوتون شیوه ترجمه اثرات خارجی وارد بر یک جسم به تغییرات سرعت آن را توضیح میدهد. بیان ریاضی این قانون معادلهی دیفرانسیل مرتبه دویی است که در یک طرف آن تغییرات تکانه جسم و طرف دیگر آن همه اطلاعات مربوط به اثرات خارجی را در قالب کمیت برداری به اسم نیرو قرار میدهد. دراینجا، تکانه جسم، حاصلضرب کمیتی ذاتی به اسم جرم جسم در سرعت آن است. جرم جسم $m$ در این قانون، پارامتری است که آهنگ تغییرات سرعت جسم $\dot{\textbf{v}}$ به واسطه نیروهای وارد شده به آن یعنی $\textbf{F}$ را کنترل میکند.
$$\textbf{F} = m \frac{d^2\textbf{x}}{dt^2} = m\dot{\textbf{v}}$$
در فیزیک رسم است که مشتق زمانی یک کمیت را با گذاشتن یک نقطه بالای آن نشان میدهیم. اینکه چرا قانون دوم توسط یک معادله دیفرانسیل مرتبه دو توصیف میشود، چیزی است که طبیعت انتخاب کرده. با این وجود این انتخاب برای ما تا حدودی خوشایند است. از لحاظ ریاضی تفسیر این معادله این است که اگر ما بدانیم بر جسمی چه نیروهایی وارد میشود و سرعت و مکان آن را در هر لحظه بدانیم، دیگر نیازی نیست اطلاعات بیشتری داشته باشیم تا حرکت آن جسم را توصیف کنیم. یعنی مکان و سرعت در یک لحظه تمام اطلاعات اولیهای است که به آنها نیاز داریم و بقیه اطلاعات دیگر را میتوانیم حساب کنیم. زیباست. نه؟!
قانون سوم نیوتون را به شیوههای مختلفی میشود بیان کرد که حتما در مورد آن شنیدهاید. آنچه که برایتان شاید جالب باشد این است که این قانون کامل نیست. منظور از کامل نبودن این است که در بعضی مسائل به تنهایی توصیف درستی ارائه نمیکند. چرا و چگونهاش بماند برای بعد. چیزی که الان مهم است این است که به واسطه قانون سوم نیوتون میشود روشی برای مقایسه و اندازه گیری جرم اجسام گوناگون پیدا کرد. پس به لطف این قانون، تکلیف جرم جسم مشخص میشود. حالا کافی است که نیروها را مشخص کنیم. آنموقع به واسطه قانون دوم میتوانیم حرکت یک جسم را توصیف کنیم. مشکل اینجاست که قوانین نیوتون به تنهایی این کار را برای ما انجام نمیدهند. یعنی در کنار این سه قانون، باید صورتبندیهایی برای نیروهای مختلف هم پیدا کنیم. خوشبختانه به نظر میرسد که تعداد نیروهای بنیادی از شمار انگشتان یک دست کمترند. در زندگی روزمره ما، نظریههای گرانش و الکترومغناطیس تقریبا همه نیروهای وارد بر اجسام را توصیف میکنند. به طور خلاصه، هر بار که چیزی میافتد به خاطر گرانش است و هر چیز دیگر تقریبا منشا الکترومغناطیس دارد از جمله بالا بردن اجسام توسط بازوی ما یا آسانسور منزل!
حالا ما میتوانیم طبیعت را توصیف کنیم. یا دست کم حرکت در طبیعت را تا وقتی که اثرات کوانتومی یا نسبیتی وارد نشدهاند را با دقت خوبی توضیح دهیم.
اما این فقط یک روایت از طبیعت است. ما میتوانیم این داستان را جور دیگری هم بیان کنیم. یعنی میشود حرکت اجسام را جور دیگری هم صورتبندی کرد بدون اینکه با صورتبندی نیوتون ناسازگار از آب درآیند. صورتبندیهایی که همین حرفها را با ریاضیات متفاوتی بیان کنند و چه بسا قدرت عمل بیشتری به ما در محاسبات و تعمیم ایدهها — فرای مکانیک استاندارد — هم دهند.

اصل کمترین کنش و روش لاگرانژ و همیلتون
فرض کنید شما سامانهای را در یک لحظه میبینید. سپس چشمانتان را برای مدت کوتاهی میبندید، دوباره باز میکنید و در لحظه جدید سامانه را در موقعیت جدیدش مشاهده میکنید. برای مثال، توپی را تصور کنید که در لحظه اول در نقطه پنالتی و در لحظه بعدی در کنج دروازه جا گرفته. حالا تمام مسیرهایی که توپ ممکن است بین این دو لحظه طی کرده باشد را تصور کنید. مثلا یک مسیر این است که توپ مستقیم از نقطه پنالتی به کنج دروازه رفته باشد. یک مسیر ممکن دیگر این است که توپ روی منحنی هیجانانگیزتری حرکت کرده و به کنج دروازه نشسته. یک مسیر هم میتواند این باشد که توپ به هوا رفته، چرخیده و دست آخر برگشته و وارد دروازه شده. حالا فرض کنید، به هر کدام از این مسیرها کمیتی نسبت میدهیم به نام کُنِش و ما کنش همه مسیرها را در جدولی یادداشت میکنیم.
هیچکس تا به حال ندیده که ضربه پنالتی به عقب برود و سپس به درواز برگردد. منطقی نیست. یا به عبارتی این مسیری نیست که طبیعت اجازه طی شدنش را بدهد وقتی شخصی به سمت دروازه ضربه میزند. پس قرارداد میکنیم که مسیری مجاز است که توسط طبیعت انتخاب شود و طبیعت مسیری را انتخاب میکند که کمترین (اکسترمم) کنش را داشته باشد. به این قاعده، اصل کمترین کنش یا اصل همیلتون میگویند. در عمل، همانطور که برای پیدا کردن نقاط اکسترمم توابع مشتق پذیر، به دنبال ریشههای مشتق آن تابع میگردیم، اینجا هم ایدههایی مشابه وجود دارد که نیاز نباشد همه مسیرها را امتحان کنیم. حالا فرض کنید که مسیری که کمترین کنش را دارد را پیدا کردهایم. پس اگر اندکی آنرا تغییر دهیم نباید کنش مسئله تغییر چشمگیری کند. درست همانطور که مثلا تابع $y = x^2$ در نقطه صفر که کمینه آن است تغییر چندانی نمیکند.
کنش $S$ را به صورت ریاضی میتوانیم به صورت انتگرال زمانی تابع دیگری به نام $L$ بنویسم. چرا؟ چون این کَلک خوبی است که در ادامه از آن لذت خواهیم برد! اسم انتگرالده را هم به احترام آقای لاگرانژ و زحماتی که برای این صورتبندی پیشتر از خیلیها انجام داده لاگرانژی میگذاریم. لاگرانژی تابعی از مکان، سرعت و احیانا زمان است. کلا بنا را هم بر این بگذارید که داریم بازی ریاضی میکنیم با این ایده که گویی لاگرانژی اطلاعات مربوط به ویژگی های ذاتی جسم و برهمکنشهای آن با دیگر ذرات و موجودات دیگر را دارد و ما میخواهیم همه این اطلاعات بین دو زمان مشخص را به کنش نسبت دهیم. پس مینویسیم
$$S = \int^{t_2}_{t_1} L(q , \dot q, t) \, dt. $$
تا اینجا هیچ کار عجیبی نکردهایم. فرض کردهایم چیزی وجود دارد به اسم کنش که به صورت یک انتگرال تعریف میشود. همینطور از مختصات تعمیم یافته $q$ و $\dot q$ برای نشان دادن مکان و سرعت استفاده کردهایم گویی میخواهیم از مختصه جدیدی به جای مثلا $x$ استفاده کنیم.
حالا میخواهیم ببینیم مسیر بهینه که اسمش را میگذاریم $q_{c(t)}$ چگونه به دست میآید. طبق چیزی که تعریف کردهایم، مسیر بهینه باید کنش را کمینه (یا به عبارت فنیتر اکسترمم) کند. پس تحت تغییرات بینهایت کوچک مسیر، کنش متناظرش نباید تغییر خاصی کند. درست مانند وقتی که مشتق توابع پیوسته — که نشاندهنده تغییرات آن توابع هستند — در نقاط بیشینه یا کمینهشان صفر هستند. پس بیاید تغییرات کنش را حساب کنیم و برابر با صفر قرار دهیم
$$ \delta S = \int^{t_2}_{t_1} dt \left( \frac{\partial L}{\partial q} \delta q + \frac{\partial L}{\partial \dot q} \delta \dot q \right) = 0. $$
با فرض این که ابتدا و انتهای مسیر را مشخص کردهایم کافی است به کمک کَلَک انتگرالگیری جز به جز ادامه دهیم.
$$ \delta S = \int_{t_1}^{t_2} dt \left( \delta q_{(t)} \frac{\partial L}{\partial q} + \frac{d}{dt} \left( \delta q_{(t)} \frac{\partial L}{\partial \dot q} \right) – \frac{d}{dt} \left( \frac{\partial L}{\partial \dot q} \right) \delta q_{(t)} \right) $$
جمله میانی به راحتی از انتگرال خارج میشود. با کنار هم قرار دادن جمله اول و سوم خواهیم داشت
$$ \delta S = \int_{t_1}^{t_2} dt \, \delta q_{(t)} \left( \frac{\partial L}{\partial q} – \frac{d}{dt} \left( \frac{\partial L}{\partial \dot q} \right) \right) + \delta q_{(t)} \frac{\partial L}{\partial \dot q} \Big|_{t_1}^{t_2} $$
جمله ی آخر صفر است چون که ابتدا و انتهای مسیر را ثابت کردهایم. البته میشد این انتخاب را انجام نداد و از جملات مرزی در مواردی استفاده کرد. اما برای این نوشته همین قدر جزئیات کافی است. از آن جا که $\delta q_{(t)}$ تغییراتی دلخواه است و برای مثال میتواند فقط در زمان دلخواه $t$ غیر صفر (تقریبا و با اغماض شبیه دلتای دیراک) باشد، انتگرالدهمان باید در هر لحظه صفر باشد. پس کمینه کردن کنش، $\delta S =0$، نتیجه میدهد
$$ \frac{\partial L}{\partial q} = \frac{d}{dt} \left( \frac{\partial L}{\partial \dot q} \right) $$
این معادله همان چیزی است که بالای سر مرد عنکبوتی وسطی ابتدای این نوشته قرار دارد و در جامعه فیزیک مشهور است به معادله اویلر–لاگرانژ. این معادله معادلات حرکت را نتیجه میدهد. درست مانند قانون دوم نیوتون.
ولی لاگرانژی واقعا چیست؟ این سوال کمابیش در زبان نیوتونی مثل آن است که بپرسیم چه نیروهایی بر جسم وارد میشوند. برای پاسخ به این پرسش نیاز به شناخت سیستم و برهمکنشهای آن داریم. مثلا برای ذرهای که در حال حرکت تحت یک پتانسیل است، لاگرانژی این سیستم برابر با با اختلاف انرژی جنبشی و پتانسیل آن ذره است. توجه کنید که لاگرانژی کمیتی نردهای است، برخلاف نیرو که کمیتی برداری است. از لحاظ ریاضی کار کردن با کمیتهای نردهای خیلی راحتتر است. این اولین حسن صورتبندی جدید است. همین طور توجه کنید که از لحاظ ابعادی، لاگرانژی بعد انرژی دارد. نکته دیگری که بد نیست بدانید این است که خیلی از اوقات لاگرانژی را بنا بر یک سری تقاضاهای فیزیکی مانند تقارن های حاکم بر سیستم حدس میزنیم. برای دیدن چند مثال در این مورد به این نوشته نگاه کنید: تقارن،قوانین پایستگی و اِمی نٌودِر.
این ویدیو سیر تاریخی این مسئله را به خوبی نشان میدهد:
منتظر ادامه این نوشته باشید.
اما اگر عجله دارید، این ویدیوها و این کتاب را نگاه کنید:
