برچسب: توزیع نرمال

همه‌ی ما قطعا بارها کلمه‌ی احتمال را شنیده‌ایم و به گوشمون خورده. توی کتاب‌های درسی هم در خیلی از سرفصل‌ها به خصوص درس جبر و احتمال با مبانی و تئوری آمار و احتمال آشنا شدیم. ولی الان میخوایم یک قدم فراتر بریم و کمی افق دیدمون رو از مسائل کلیشه‌ای که قبلا تو کتاب‌هامون دیدیم فراتر ببریم. بنا داریم به یکی از مهمترین نتایجی که از دل نظریه‌ی آمار و احتمال بیرون میاد بپردازیم و این نتیجه چیزی نیست جز قضیه‌ی حد مرکزی یا همون ‌Central Limit Theorem.

شاید به گوشتون خورده باشه که تابع توزیع بعضی از فرآیندهایی که در طبیعت رخ می‌دهد نرمال یا گاوسی هست و حالا ما میخواهیم ببینیم چرا و چگونه؟!

خب قبل از هر چیز ببینیم چرا به این قضیه میگن حد مرکزی. در دایره‌ی آمار، اطلاعات و احتمالات نقش مرکز رو داره و بسیاری از محاسبات بر اساس این قضیه انجام میشه. از طرفی صورت مجانبی داره و برای حد نمونه‌های بزرگ درست هست و خیلی خوب کار می‌کنه. از همین رو و به خاطر این دو دلیل میشه حد مرکزی.

اولین اطلاعاتی که ما می‌تونیم از یک فرآیند که مجموعه‌ای از متغیرها در اون وجود دارند بدست آوریم از تابع توزیع اون فرآیند بدست میاد. مثلا تابع توزیع احتمال بیانگر احتمال هر کدوم از متغیرهای تصادفی و یا احتمال قرار گرفتن هر متغیر در یک بازه‌ی معلوم هست که اولی برای متغیرهای گسسته و دومی برای متغیرهای پیوسته تعریف می‌شود.

صورت قضیه : تابع توزیع متغیر تصادفی که خودش از جمع $n$ تا متغیر تصادفی دیگه که دارای تابع توزیع $p(x)$ و واریانس محدود $\sigma_{i}$هستند، به سمت تابع توزیع گاوسی میل می‌کند.

یعنی متوسط گیری در تعداد زیاد (نگاه آماری ما به مساله) به سمت توزیع گاوسی متمایل میشه. بدون اینکه مهم باشه مجموعه‌های تصادفی تشکیل دهنده، خود دارای چه تابع توزیعی هستند. پس یک نکته‌ی خیلی خوب و مفید اینه که بدون داشتن اطلاعات اولیه میشه تا حد خوبی تابع توزیع رو روی جمع متغیرهای تصادفی تعیین کرد. حتی اگر متغیرهای اولیه‌ی ما خودشون هم دارای تابع توزیع مشخصی باشند، متوسط گیری روی اونها به سمت تابع توزیع گاوسی متمایل میشه، با اینکه مستقل از هم اندازه‌گیری می‌شوند.

یکی از مثال‌های ملموس در این زمینه :

زمانی که یک لودر خاکی را در یک پروژه‌ی عمرانی جابجا می‌کند و در یک نقطه تخلیه می‌کند، انتظار داریم خاک‌های ریخته شده شبیه یک تپه شود. یک تل از خاک شبیه یک تابع توزیع گاوسی دو بعدی است. هر فرآيندی که در طبیعت رخ می‌دهد، به شرطی که انحراف از معیار اون واگرا نباشد و عامل خارجی هم تصادفی بودن توزیع رو بهم نزنه، در نهایت توزیع به سمت تابع توزیع گاوسی میل می‌کند.

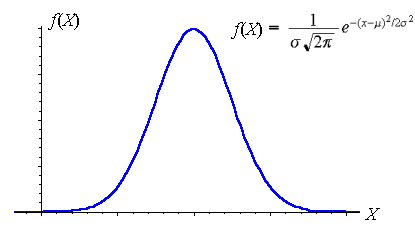
 عکس زیرنمونه‌ای از تابع توزیع گاوسی یا همان نمودار زنگوله‌ای رو نشان می‌دهند.($\mu$ مقدار متوسط است)

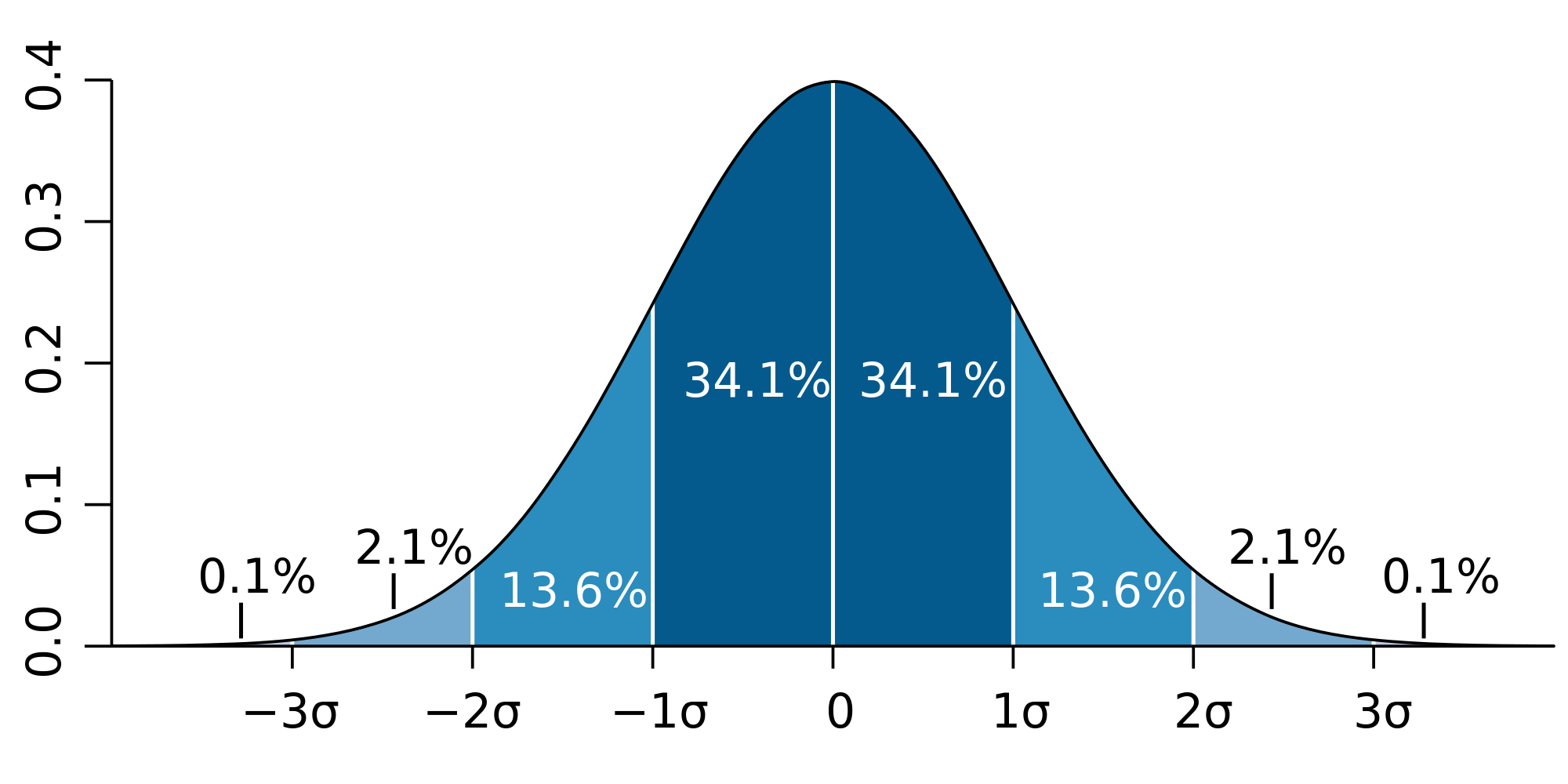
توی این شکل هم می‌توان به نوعی تجمع داده‌ها در زیر نمودار تابع توزیع نرمال مشاهده کرد که نشون‌دهنده‌ی تجمع داده‌ها حول مقدارمتوسط هست.

 

برای مطالعه‌ی بیشتر در مورد این قضیه و همچنین آشنایی بیشتر با مبانی آمار و احتمال می‌تونید سری به منابع زیر بزنید:

• Feller, W. “The Fundamental Limit Theorems in Probability.” Bull. Amer. Math. Soc. 51, 800-832, 194
• Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. New York: Wiley, p. 229, 1968
• Spiegel, M. R. Theory and Problems of Probability and Statistics. New York: McGraw-Hill, pp. 112-113, 1992
• Zabell, S. L. “Alan Turing and the Central Limit Theorem.” Amer. Math. Monthly 102, 483-494, 1995
• Trotter, H. F. “An Elementary Proof of the Central Limit Theorem.” Arch. Math. 10, 226-234, 1959