نان تُست همیشه از سمتِ کرهایاش روی زمین میافتد و گربهها هم همیشه روی پاهایشان فرود میآیند؛ اما این تضادِ بامزه، درواقع تنها یک شوخی ذهنی است. با این حال، تواناییِ واقعیِ گربهها در اینکه هنگام سقوط، بدنشان را بچرخانند و روی پا فرود آیند، شوخی نیست. این مسئله سالها ذهن دانشمندان را به خود مشغول کرده بود، چرا که به نظر میرسید با یکی از اصول مهم فیزیک، یعنی «پایستگی تکانه زاویهای»، ناسازگار باشد. اگر گربه را به شکل استوانهای صُلب تصور کنیم، چنین جسمی هنگام سقوط نمیتواند ناگهان تکانه زاویهای تولید کند؛ ولی گربهها این کار را به سادگی انجام میدهند.
در سال ۱۹۷۵، جک هدرینگتون، مقالهای نوشت و در سراسر آن از ضمیر «ما» استفاده کرد. وقتی سردبیر ژورنال اعلام کرد که باید نویسندهٔ دوم نیز وجود داشته باشد، هدرینگتون برای آنکه مجبور به تایپ دوبارهٔ مقاله نشود، اسم گربهاش «چستر» را بهعنوان همکار نویسنده درج کرد. اکنون این گربه یک پروفایل رسمی با اسم اِف. دی. سی. ویلارد در گوگل اسکالر دارد که نشان میدهد مقالاتش تا امروز ۱۱۳ بار مورد استناد پژوهشگران دیگر قرار گرفته است!
گربهها موجودات عجیبی هستند. از هر جایی و هر طوری که رهایشان کنی، دست آخر روی پنجه فرود میآیند. بدن گربه نه یک استوانهٔ صُلب، بلکه مجموعهای انعطافپذیر از دو بخشِ جداگانه است که میتواند در جهات مخالف یکدیگر خم شود و بچرخد. چگونگی انجام این کار، اولین بار در سال ۱۹۶۹ توسط یک مدل ریاضی توضیح داده شد. انعاطفپذیری زیاد گربهها و اینکه در هر ظرفی جا میشوند و شکل آن را به خود میگیرند هم سبب شده تا مردم به شوخی بگویند گربه مایع است. ارک-آنتوان فاردین، در مقالهای با عنوانِ «گربههای مایع»، از آنها برای توضیح چند مفهوم پایهای در رئولوژی (مطالعه جریان و تغییر شکل مواد) استفاده کند. این پژوهش شوخطبعانه باعث شد فاردین در سال ۲۰۱۷ جایزهٔ ایگ نوبل فیزیک را دریافت کند.
اما در دنیای فیزیک، مشهورترین گربه، «گربهٔ شرودینگر» است. این آزمایش فکری را اروین شرودینگر، ابتدا برای انتقاد از «تفسیر کپنهاگی مکانیک کوانتومی» مطرح کرد. هدف او تأکید بر تناقضی بود که در قلب نظریهٔ کوانتوم وجود داشت: گربهای که همزمان هم زنده و هم مرده است. شرودینگر شاید صرفاً به دنبال تأکید بر یک نکتهٔ عجیب و غیرمعمول بود؛ اما برهمنهیِ کوانتومی که گربهٔ فرضیاش توصیف میکند کاملاً واقعی است.
در فیزیکِ نور میتوان دو حالت نوری را که فازهای متفاوت و متضادی دارند با هم ترکیب کرد و وضعیتی به نام «حالت گربهای» ساخت. اگر شدت نور در چنین حالتی اندک باشد، به آن «حالت بچهگربهای» میگویند. این «حالتهای گربهای» صرفاً کنجکاوی نظری نیستند؛ آنها کاربردهایی جدی در حوزهٔ اطلاعات کوانتومی دارند. برای نمونه، «کدهای گربهای» یکی از روشهای معروف برای تصحیح خطا در رایانش کوانتومی هستند.
در داستان آلیس در سرزمین عجایب، «گربهٔ چشایر» میتواند بهتدریج ناپدید شود و تنها لبخندش را در هوا باقی بگذارد. اخیراً دانشمندان حالتی کوانتومی به نام «گربهٔ چشایرِ کوانتومی» را شناسایی کردهاند که در آن ویژگیهای یک ذره (مانند تکانهٔ مغناطیسی) میتواند از خودِ ذره جدا شده و در مسیر متفاوتی حرکت کند. این گربههای عجیب حتی میتوانند ویژگیهایشان (مانند همان لبخند معروف) را با هم مبادله کنند!
- The physics of cats. Nat Rev Phys 7, 165 (2025)
https://doi.org/10.1038/s42254-025-00824-6





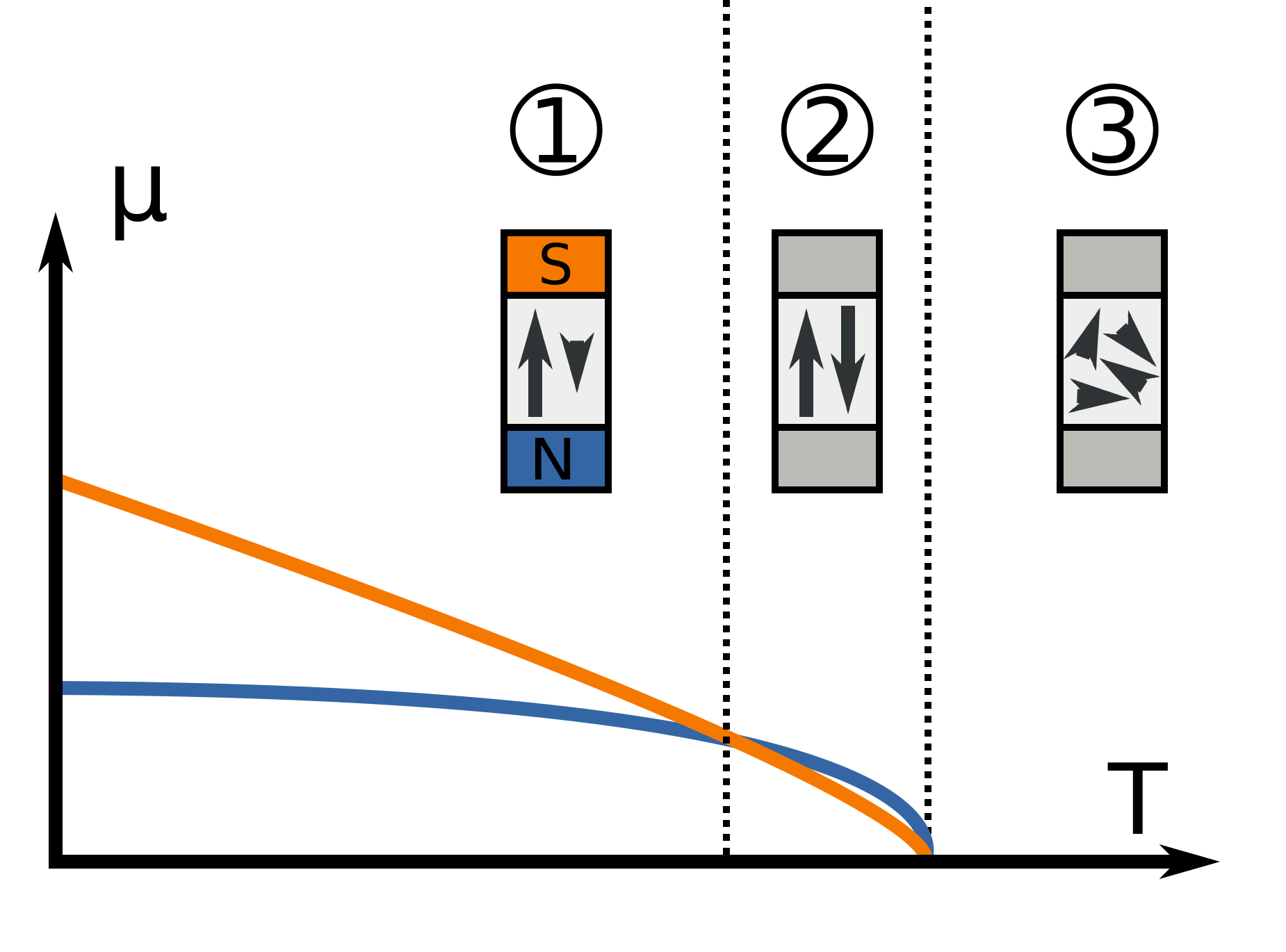
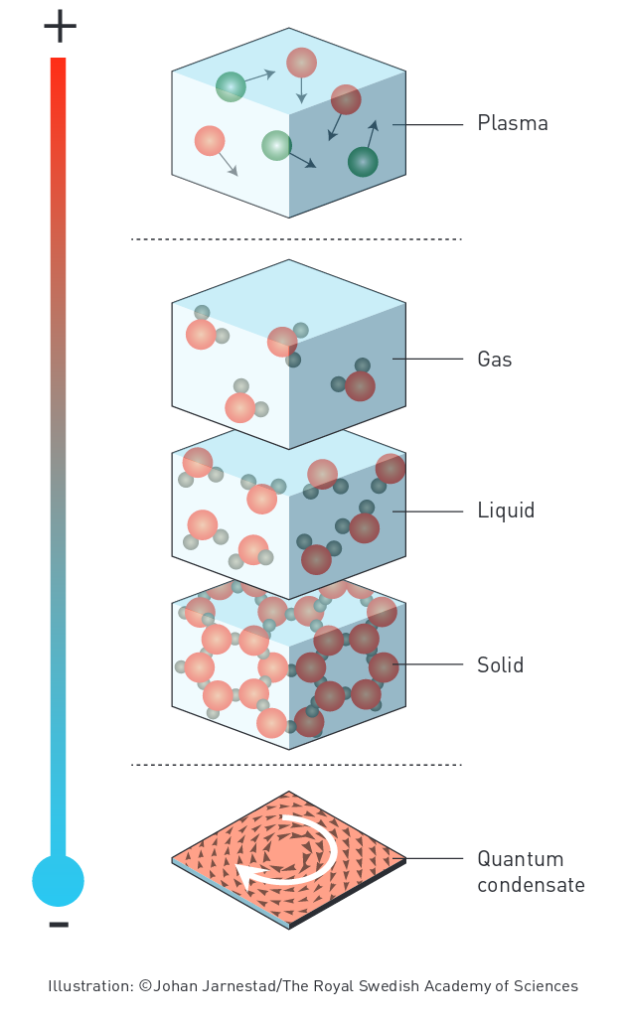
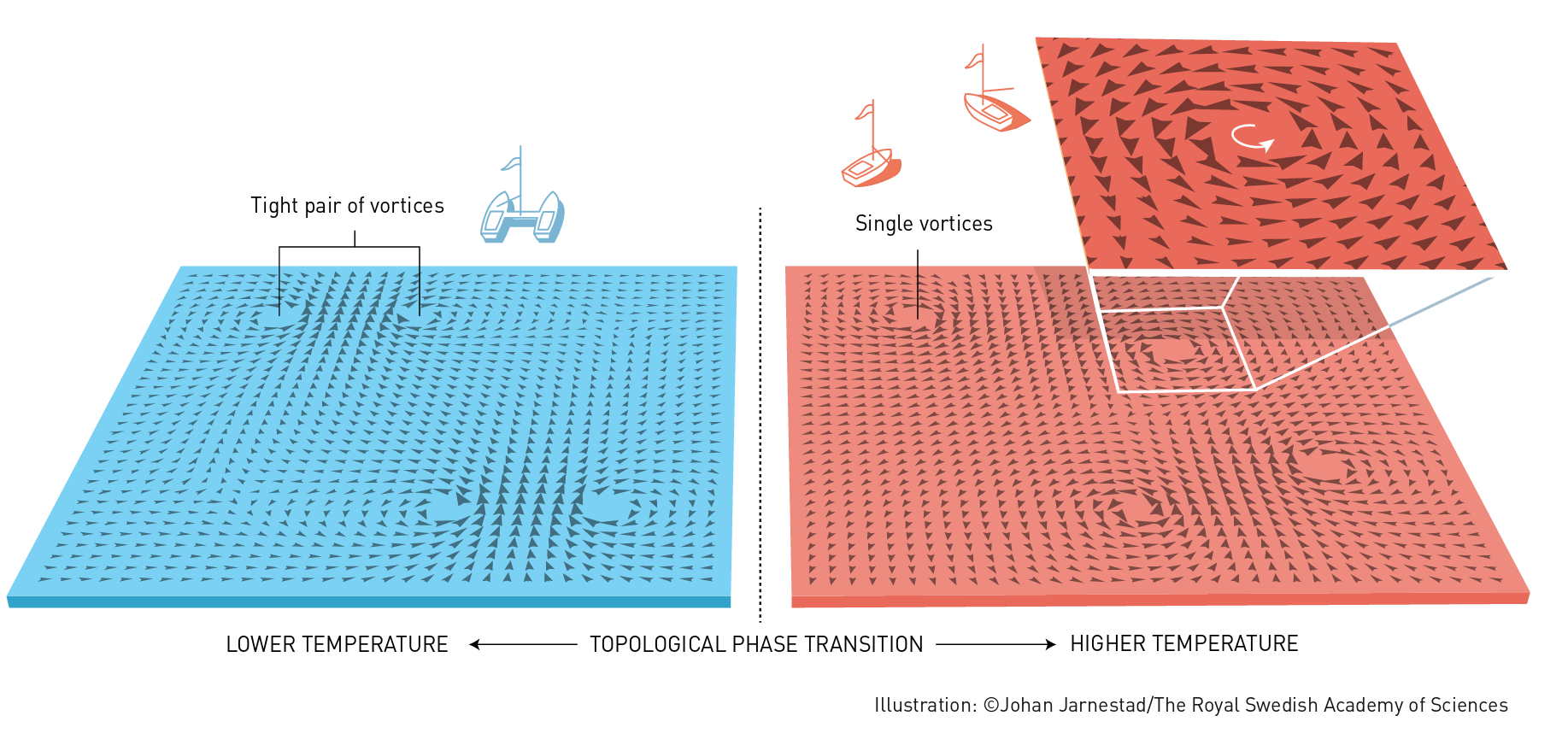
 یه گذار روزمره مثل تغییر فاز آب رو در نظر بگیرید. گاز و مایع به واقع شبیه هم هستن! هر دو از نظر ما بی نظم هستن! حالا یکی یه کم بیشتر یکی یه کم کمتر. اما هیچ کدوم جامد منظم نیستن که همه سرجاشون نشسته باشن.
یه گذار روزمره مثل تغییر فاز آب رو در نظر بگیرید. گاز و مایع به واقع شبیه هم هستن! هر دو از نظر ما بی نظم هستن! حالا یکی یه کم بیشتر یکی یه کم کمتر. اما هیچ کدوم جامد منظم نیستن که همه سرجاشون نشسته باشن.