پاره شدن نخ‌های واسطه بین چند جرم آویزان

فرمول‌بندی مسئله

$n$ جسم و $n+1$ نخ آن‌طور که در شکل ۱ نشان داده شده است را در نظر می‌گیریم. جرم هرکدام از اجسام را برابر $m$ و نخ‌ها را بی جرم فرض می‌کنیم. همان‌طور که در شکل مشخص است، سیستم در شتاب گرانش $g$ قرار دارد. به نخ پایین نیروی ثابت $F$ را وارد می‌کنیم به‌طوری که شتاب ثابت $a$ را به سمت پایین به انتهای نخ آخر بدهد. برای به‌دست آوردن زمان پاره شدن نخ‌ها، ابتدا $x_i(t)$ها را که در شکل مشخص شده‌اند به‌دست می‌آوریم. بعد از این کار کافی است فرض کنیم که اگر نخ‌ها به‌اندازه $\Delta l$ کشیده شوند پاره می‌شوند.

برای بررسی حرکت دستگاه، نخ‌ها را به‌صورت فنرهایی با طول اولیه $l_0$ و ثابت $k$ در نظر می‌گیریم. وقتی این مجموعه را به‌طور قائم بیاویزیم، طول نخ $p$ام (از بالا) به‌اندازه $\Delta l_p = (n-p+1)mg/k$ افزایش می‌یابد که ناشی از وزن اجسام است. در این حالت با انتخاب نقاط مرجع مناسب می‌توانیم تابع انرژی پتانسیل را به‌صورت زیر تعریف کنیم.

$$U(x_1, x_2, \cdots, x_n, y) = \sum_{i=1}\left[ \frac{1}{2}k(x_i \mathbin{-} x_{i-1} + \Delta l_i)^2 \mathbin{-} mgx_i \right] + \frac{1}{2}k(y \mathbin{-} x_n)^2. \quad (۱)$$

توجه کنید که $x_p(t)$ از محل تعادل جرم شماره $p$ (از بالا) و $x_0=0$ در نظر گرفته شده. در واقع در این حالت جملات ثابتی نیز باید در انرژی پتانسیل دستگاه در نظر گرفت که به علت عدم تأثیر در معادلات حرکت از نوشتن آن‌ها صرف‌نظر کرده‌ایم.

با توجه به اینکه $m\ddot{x}_p = -\partial U / \partial x_p$، معادلات حرکت را می‌توان چنین نوشت:

$$m\ddot{x}_1 + k(2x_1\mathbin{-} x_2) = 0,$$ $$m\ddot{x}_p + k(2x_p\mathbin{-} x_{p-1} \mathbin{-} x_{p+1}) = 0, \quad (۲)$$ $$m\ddot{x}_n + k(x_n \mathbin{-} x_{n-1} \mathbin{-} y) = 0.$$

چون شتاب ثابت است، $y = (1/2)at^2$ و بنابراین می‌توانیم جواب‌های معادلات بالا را چنین بنویسیم:

$$x_p(t) = \sum_{j=1}^{n} \big(A_{pj} \cos(\omega_j t) + B_{pj} \sin(\omega_j t)\big) + C_{p1}t^2 + C_{p2}t + C_{p3}.$$

با جایگذاری جواب‌هایی به شکل فوق در دستگاه معادلات (۲) به‌دست می‌آوریم $\omega_j^2 =(k/m)\lambda_j$، آن‌گاه $\lambda_j$ها جواب‌های معادله زیرند:

$$(2 \mathbin{-} \lambda)\left(2 \mathbin{-} \lambda \mathbin{-} \frac{1}{2 \mathbin{-} \lambda}\right)\left(2 \mathbin{-} \lambda \mathbin{-} \frac{1}{2 \mathbin{-} \lambda \mathbin{-} \frac{1}{2 \mathbin{-} \lambda}}\right) \dots = 0.$$

همچنین $C_{p1} = (pa/2(n+1))$ و $C_{p2}=0$ است. $C_{p3} = (map/6k(n+1))(p^2-n(n+2)-1)$ و با توجه به شرایط اولیه $x_p(0) = \dot{x}_p(0) = 0$، ضرایب $A_{pj}$ و $B_{pj}$ نیز مشخص می‌شوند. با مشخص شدن $x_j(t)$ها، می‌توانیم معادلات مربوط به پاره شدن نخ‌ها را به‌دست آوریم. برای این کار کافی است فرض کنیم که وقتی نخ‌ها به‌طور مشخص $L$ می‌رسند پاره می‌شوند. پس زمان پاره شدن نخ‌ها را باید از روابط زیر به‌دست آوریم:

$$x_1 + l_0 + l_1 = L,$$ $$\vdots$$ $$(x_p \mathbin{-} x_{p-1}) + l_0 + l_p = L, \quad (۳)$$ $$\vdots$$ $$(y\mathbin{-} x_n) + l_0 = L.$$

زمان پاره شدن نخ $p$ام، $t_p$، با قرار دادن $x_{p-1}$ و $x_p$ در معادلهٔ $p$ام (از بالا) دستگاه معادلات (۳) و حل آن به‌دست می‌آید. با مقایسهٔ مقادیر زمان‌های لازم برای پاره شدن نخ‌ها می‌توانیم نخی را که در اثر کشیدن انتهای پایینی مجموعه پاره می‌شود مشخص کنیم. از آن‌جا که که بررسی جواب‌ها حتی در حالت $n=1$ به سبب وجود جملات مثلثاتی کار آسانی نیست از روش‌های عددی استفاده می‌کنیم و مسئله را در حالت‌های خاص (یک و دو جسم) بررسی می‌کنیم.

حالت خاص n=1

فرض کنید فقط یک جسم داریم. این مسئله معمولاً در درس مکانیک مقدماتی برای دانشجویان مطرح می‌شود و به‌طور کیفی نیز به آن پاسخ داده می‌شود. در اینجا به حل کمی این مسئله می‌پردازیم. در این حالت، معادله حرکت جسم چنین است:

$$x(t) = \frac{a}{2\omega^2} \left( \cos(\omega t) \mathbin{-} 1 \right) + \frac{a}{4} t^2, \quad \omega^2 = \frac{2k}{m}.$$

پس معادلات مربوط به زمان پاره شدن نخ‌ها چنین‌اند ($l = mg/k$):

$$\Delta l \mathbin{-} l = \frac{a}{2\omega^2}( \cos(\omega t_1)\mathbin{-} 1) + \frac{a}{4}t^2_1, \quad (۴)$$ $$\Delta l = \frac{-a}{2\omega^2}( \cos(\omega t_2)\mathbin{-} 1) + \frac{a}{4}t^2_2.$$

پارامترهای مؤثر در زمان پاره شدن نخ $k/m$ ، $\Delta l$ و $a$ هستند. ابتدا حالتی خاص را بررسی می‌کنیم. فرض کنید $k/m$ هزار بر مجذور ثانیه و $\Delta l$ دو میلی‌متر باشد. این مقادیر گستره بزرگی از حالت‌های معمول و قابل آزمایش در مورد این مسئله را در بر می‌گیرند. با حل عددی و به‌دست آوردن $t_1$ و $t_2$ از معادلات (۴) به‌ازای این مقادیر $k/m$ و $\Delta l$ و برای چندین شتاب مختلف نمودار شکل ۲ به‌دست می‌آید. این نمودار نشان می‌دهد که (برای شتاب‌هایی در بازه مشخص شده در شکل) برای شتاب‌های به‌اندازه کافی بزرگ، نخ پایینی و برای شتاب‌های کم، نخ بالایی پاره می‌شود این نتیجه‌گیری با درک شهودی ما از مسئله کاملاً توافق دارد.

اکنون شتاب مربوط به نقطه برخورد در این حالت را پیدا می‌کنیم. فرض کنید $t=t_1=t_2$. دو طرف معادلات (۴) را با هم جمع می‌کنیم و $t$ را به‌دست می‌آوریم. اکنون اگر مقدار $a$ در $t=2\sqrt{(2\Delta l \mathbin{-} l)/a}$ را در یکی از معادله‌ها قرار دهیم و تعریف کنیم $\beta = \sqrt{\left(\frac{\Delta l}{l} \mathbin{-} 1\right)}$ و $\alpha = \sqrt{\frac{a}{4g}}$ نتیجه می‌شود:

$$\alpha^2(\cos(\beta/\alpha) \mathbin{-} 1 ) + \frac{1}{2} = 0. \quad (۵)$$

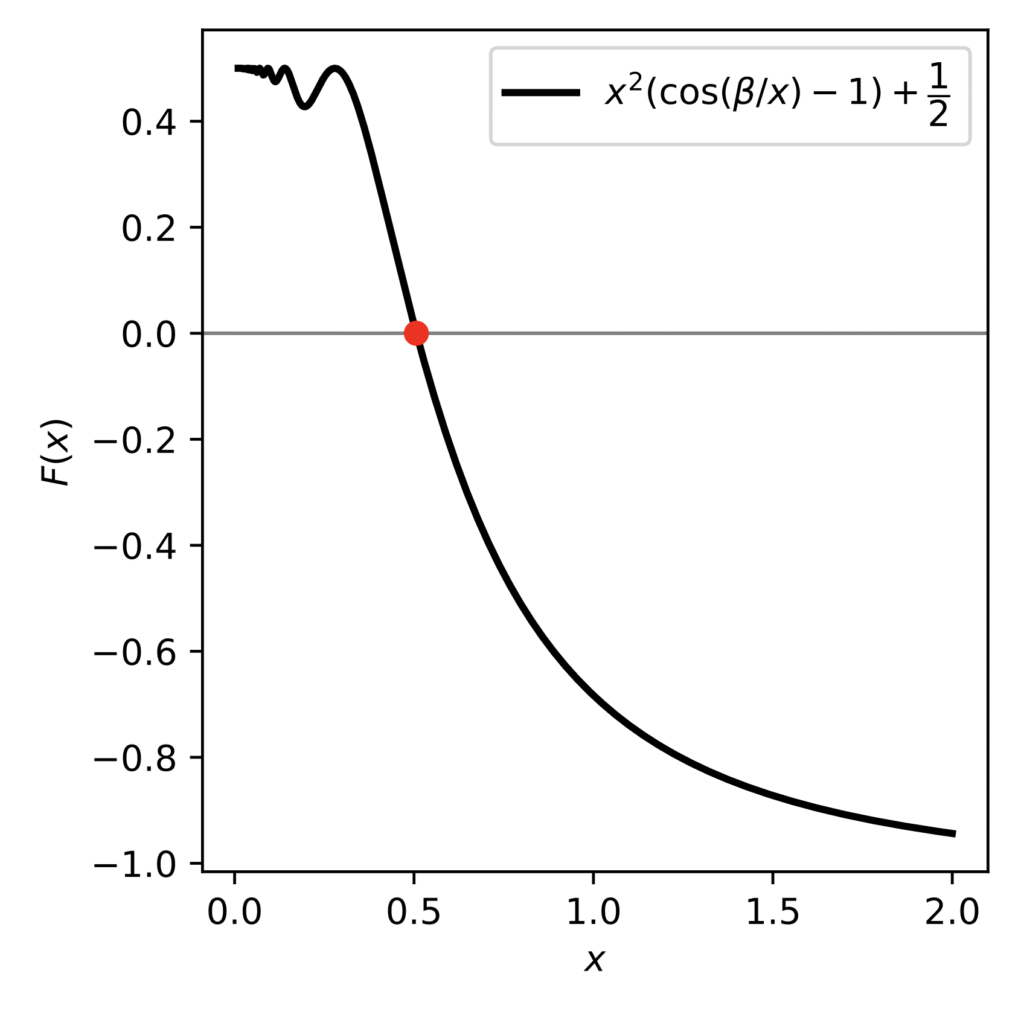
نمودار تابع $F(x) = x^2\big(\cos(\beta/x) \mathbin{-} 1 \big) + \frac{1}{2}$ در شکل ۳ برای حالتی که در آن $\beta = \beta_1 \approx 1.755$ رسم شده است. با حل معادله $F(x) = 0$ (به وسیله کامپیوتر)، ریشه $0.507$ (که در شکل ۳ مشخص شده است) به دست می آید. یعنی شتاب لازم برای پاره شدن همزمان نخ‌ها تقریبا ده متر بر مجذور ثانیه است. که با نمودار شکل ۲ توافق دارد.

برای اینکه ثابت کنیم معادله $F(x) = 0$ فقط همین یک ریشه را دارد، کافی است ثابت کنیم که $F'(x)$ به ازای مقادیر $x$ بزرگتر از $\alpha$ نزولی است. این کار را می‌توان با محاسبه $F'(x)$ و تقریب زدن $\cos(\beta/x)$ و $\sin(\beta/x)$ با چند جمله از بسط سری آن‌ها به سادگی نشان داد. بنابراین $F(x) = 0$ فقط یک ریشه دارد.

اکنون نشان می‌دهیم که در همه حالتهای مورد بحث، موضوع به همین شکل است. یعنی همواره یک نقطه برخورد وجود دارد که برای شتاب‌های کوچکتر از شتاب آن نقطه، نخ بالایی و برای شتاب‌های بزرگتر از شتاب آن نقطه، نخ پایینی پاره می‌شود. ابتدا این موضوع را که معادله ۵ یک و فقط یک ریشه دارد، به مقادیر منطقی و مورد بحث در این مقاله تعمیم می‌دهیم (منظور از مقادیر مورد بحث $\beta$ بعدا مشخص می‌شود). فرض کنید که بخواهیم معادله (۵) را برای $\beta \approx \beta_2$ بررسی کنیم. اگر $d=\beta_2/\beta_1$ و $\beta_1 = 1.755$ در این صورت با تغییر متغیر $X = x/d$ حل معادله مورد نظر متناظر با یافتن ریشه $H(X)=0$ است که در آن

$$H(X) = X^2(\cos(\beta_1/X) \mathbin{-} 1 ) + \frac{1}{2d^2}.$$

نمودار تابع $H$ از انتقال تابع $F$ به دست می‌آید. ولی نمودار $F(x)$ اگر تا جایی به پایین انتقال پیدا کند که قسمت تناوبی آن بالای محور $x$ قرار گیرد، نمودار فقط در یک نقطه با این محور برخورد خواهد کرد. با توجه به شکل ۳ می‌توان دریافت که اگر انتقال حدوداً کمتر از $0.4$ واحد باشد یعنی اگر $(1/2) \mathbin{-} (1/2d^2) \leq 0.4$، این برخورد صورت نمی‌گیرد. این شرط با توجه به اینکه در نمودار شکل ۲ داریم $\Delta l/l \approx 2$ متناظر با این است که $\Delta l/l \leq 8$ باشد.

اما در چه حالت‌هایی بیش از یک نقطه برخورد وجود دارد؟ $\Delta l/l>8$ نشان می‌دهد که افزایش طول لازم برای پاره شدن نخ، هشت برابر طولی است که در ابتدا با وصل کردن جسم به آن داده می‌شود. این موضوع نشان می‌دهد که مقدار کش آمدن نخ و یا ثابتی که برای آن انتخاب کرده‌ایم در مقابل جسم جرم آنقدر زیاد است که تاثیر جسم در پاره شدن نخ، که به صورت جمله نوسانی و مقدار $l$ در معادلات ظاهر می‌شود، تقریبا از بین می‌رود. زیرا اگر $\Delta l$ بسیار بزرگتر از $l$ باشد، از معادلات (۴) نتیجه می‌شود که تاثیر وجود جسم، که به صورت جمله کسینوس و همچنین کاهش مقدار کششی لازم برای پاره شدن نخ بالایی از $\Delta l$ به $\Delta l \mathbin{-} l$ ظاهر می‌شود، رفته رفته از بین می‌رود. بنابراین فقط حالت‌هایی را بررسی می‌کنیم که نسبت $\Delta l/l$ در حدی باشد که نقش وجود جسم در پاره شدن نخ کاملاً مشخص باشد. به همین دلیل است که در ابتدا جرمی بین دو نخ در نظر می‌گیریم و دستگاه را به طور قائم در شتاب گرانش قرار می‌دهیم.

تا اینجا مشخص شد که به ازای تمامی حالتهایی که جسم — با تقریب ما برای آن‌ها — وجود دارد، یک و فقط یک شتاب $a_0$ موجود است که هر نخ را همزمان پاره می‌کند. اکنون اگر نشان دهیم که شتابهایی مانند $a_1$ و $a_2$ وجود دارند که به ازای $a_c < a_1$ و $t_1 > t_2$ و به ازای $a_c >a_2$ و $t_1 < t_2$ آنچه می‌خواهیم به آسانی ثابت می‌شود. اگر معادلات (۴) را به صورت زیر بنویسیم:

$$\frac{\Delta l \mathbin{-} l}{a} + \frac{1}{2\omega^2} \big(\cos(\omega t_1) – 1\big) = \frac{1}{4}t_1^2,$$ $$\frac{\Delta l}{a} + \frac{1}{2\omega^2} \big(\cos(\omega t_2) – 1\big) = \frac{1}{4}t_2^2.$$

چون جمله کسینوس کراندار است با کم کردن $a$ برای مقادیر ثابت $\omega, l, \Delta l$ تاثیر این جمله کم و بیش از بین می‌رود، بنابراین همیشه می‌توانیم $a <a_0$ را آنقدر کوچک بگیریم که این جمله در معادلات قابل چشم پوشی
باشد. در این صورت $t_1 = 2\sqrt{(\Delta l \mathbin{-} l)/a}$ و $t_2 = 2\sqrt{\Delta l/a}$. پس همواره از$a <a_0$ نتیجه می‌شود $t_1 <t_2$.

حالا فرض کنید که $t_1$ و $t_2$ در معادله (۴) بسیار کوچک باشند، به طوری که بتوانیم بسط سری کسینوس را به صورت زیر بنویسم:

$$\Delta l \mathbin{-} l \approx (1 \mathbin{-} \frac{\omega^2 t_1^2}{2} + \frac{\omega^4 t_1^4}{4}\mathbin{-}1) \frac{a}{2\omega^2} + \frac{1}{4}at_1^2, \quad (۶)$$ $$\Delta l \approx \frac{\omega^2 t_2^2}{2} \frac{a}{2\omega^2}+ \frac{1}{4}at_2^2$$

در این صورت، این جواب‌ها به‌دست می‌آیند: $t_{1} = \sqrt[4]{\frac{48\,(\Delta l \mathbin{-} l)}{a\,\omega^2}}$ و $t_{2} = \sqrt{\frac{2\,\Delta l}{a}}$.

با توجه به فرض بسیار کوچک بودن $t_{1}$ و $t_{2}$ و این‌که $a$ برای جواب هر دو زمان در مخرج ظاهر شده است، نتیجه می‌گیریم که برای مقادیر بسیار بزرگ $a$، جواب‌های (۴) با تقریب خوبی به شکل (۶) هستند. با توجه به جواب $t_{1}$ و $t_{2}$ اگر $a<a_c$ آنگاه $t_2<t_1$ به طوری که $a_c =
 \frac{\Delta l^2 \omega^2}{2(\Delta l \mathbin{-} l)}$. پس برای شتاب‌های بزرگ و زمان‌های کوچک می‌شود دید که $t_2<t_1$.

بنا بر آن‌چه گفته شد، با فرض اینکه نمودار جواب‌های (۴) در محدودهٔ مورد بررسی ناپیوستگی‌های قابل ملاحظه‌ای نداشته باشد (که فرض معقولی است) می‌توانیم این نتیجه‌گیری کلی را بکنیم که برای شتاب‌های به اندازهٔ کافی بزرگ نخ پایین و برای شتاب‌های کوچک، نخ بالایی پاره می‌شود. این مطابق با جوابی است که به صورت شهودی به این مسئله داده می‌شود.

حالت خاص n=2

برای دو جسم، معادلات زیر را در مورد زمان پاره شدن نخ‌ها به‌دست آوریم:

$$\Delta l \mathbin{-} l_1= \frac{a}{2\omega_1^2} \cos(\omega_1 t_1)\mathbin{-}\frac{a}{6\omega_2^2} \cos(\omega_2 t_1)+\frac{1}{6}at_1^2 \mathbin{-} \frac{4a}{9\omega_1}),$$ $$\Delta l \mathbin{-}l_2 = \frac{a}{3\omega_2} \cos(\omega_2 t_2) +\frac{1}{6}at_2^2\mathbin{-}\frac{a}{9\omega_1^2},$$ $$\Delta l = \frac{1}{6}at_1^2 \mathbin{-} \frac{a}{2\omega_1^2}\cos(\omega_1t_3)\mathbin{-} \frac{a}{6\omega_2^2}\cos(\omega_2t_3) + \frac{5}{9\omega_1^2}a. \quad (۷)$$

که در این معادلات $\omega_1^2 = \frac{k}{m}, \omega_2^2 = \frac{3k}{m}, l_1 = \frac{2mg}{k}, l_2 = \frac{mg}{k}$.

مشخص است که معادلات (۷) نسبت به حالت $n=1$ بسیار پیچیده‌ترند و بحث در مورد آن‌ها بسیار دشوارتر از حالت قبل است. در این حالت، به بررسی جواب‌ها فقط در یک مورد خاص بسنده می‌کنیم.

دوباره مقادیر قبلی را برای $\Delta l$ و $k/m$ در نظر بگیرید. اگر جواب‌های (۷) را برای شتاب‌های مختلف با کمک کامپیوتر به‌دست بیاوریم، به نمودار شکل ۴ می‌رسیم. در این نمودار رفتار شتاب تا $50 \text{ms}^{-2}$ بررسی شده است. این نمودار نشان می‌دهد که در شتاب‌های معمولی نخ وسطی پاره نمی‌شود. حل عددی به ما نشان می‌دهد که شتاب لازم برای کوچک‌تر شدن $t_2$ از $t_3$ در حدود ۲۵۰ متر بر مجذور ثانیه است و برای این‌که $t_2$ از $t_1$ کوچکتر شود شتاب بسیار بیشتر که منطقی نیست لازم است. بنابراین آنچه که ما در شتاب‌های معمولی می‌بینیم این است که مانند حالت $n=1$ برای شتاب‌های به‌اندازه کافی کوچک، نخ بالایی و برای شتاب‌های بزرگ نخ پایینی پاره می‌شود.

نتیجه‌گیری

نتایجی که در پایان حالت‌های خاص گرفته شد، یعنی پاره شدن نخ بالایی برای شتاب‌های کم و نخ پایینی برای شتاب‌های زیاد، با درک فیزیکی ما از مسئله کاملاً سازگار است. جواب‌هایی که در کلاس‌های درس مکانیک به حالت $n=1$ داده می‌شود بیشتر جنبه کیفی دارد ولی آنچه ما در اینجا نشان دادیم، بیانگر این موضوع است که این جواب‌های کیفی با حل کمی نیز تأیید می‌شوند. در طول حل مسئله مواردی پیش آمد که به منظور جلوگیری از پراکنده شدن مطلب اصلی، اقدام به بیان دقیق و بررسی جزئیات و انجام اعمال ریاضی نکردیم؛ دقیق‌تر کردن این موارد با کسی حوصله‌مند امکان‌پذیر است (نویسنده این کار را انجام داده است). در هر صورت با وجود ایرادهایی که به فرض‌های اولیه ما وارد است، مثلاً این‌که طبیعت نخ‌ها مخصوصاً در آستانه پاره شدن به صورت یک فنر ایده‌آل که ما فرض کردیم رفتار نمی‌کنند و یا فرضیه‌هایی مانند برابر بودن جرم اجسام و یا ثابت بودن شتاب پایین کشیدن نخ‌ها که از کلیت مسئله می‌کاهد، موضوع جالب توجه اینجاست که جواب به‌دست آمده با تقریب در نظر گرفتن نخ‌ها به‌صورت فنر در محدوده مورد بررسی، کاملاً با تجربه سازگار است و شهود کیفی ما را از مسئله تأیید می‌کند.

سپاسگزاری

در اینجا لازم است از آقای دکتر محمود بهمن‌آبادی که برای حل این مسئله از راهنمایی‌های ارزنده ایشان استفاده کرده‌ام تشکر کنم.