شاید در سال ۱۹۶۲ که ماکس پروتز آلمانی و سر جان کندرو انگلیسی جایزه نوبل شیمی را برای مطالعه در باب پروتئین ها و ساختارکرویشان دریافت کردند هرگز تصور نمیکردند که دنیای پروتئینها پر از رموز کشف نشده و جذاب باشد. اما اکنون با گذشت بیش از ۵۰ سال از از آن روزها دنیای پروتئینها جذاب تر از چیزی به نظر میرسد که دانشمندان بدان فکر میکردند. یکی از بحثهای جالبی که امروز در دنیای علم بسیار هم مورد توجه قرار گرفتهاست، فیزیک پروتئینهاست به ویژه مسالهی تاشدگی پروتئینها یا همان پروتئین فولدینگ. تو این پست بنا داریم یکمی بیشتر با اتفاقاتی که توی سلولهای بدنمون توسط پروتئینها رقم میخوره آشناشویم.
وقتی اسم پروتئین به وسط میآید اولین چیزی که به ذهنمان میرسد احتمالا گوشت و مرغ و ماهی است. ما گوشت و مرغ مصرف میکنیم که پروتئین لازم برای بدن تأمین شود غافل از اینکه مونومر آمینواسیدهای بدنمون قابلیت ساخت بسیاری از پروتئینها رودارند. اما یکی از مسائلی که بسیار مورد توجه محققان میانرشتهای قرار گرفته مسالهی پروتئین فولدینگ است. اما چه شد که این مساله مهم شد. اصلاً پروتئین فولدینگ یعنی چه؟ این فرآیند یک فرآیند فیزیکی است که در آن پلیپپتایدها(Polypeptide) که همان پلیمرهایی هستند که از به هم پیوستن آمینواسیدها حاصل میشوند، به یک ساختار مشخص سه بعدی میرسند. پلیپپتایدها زنجیرهای از اسیدهای آمینه هستند و درواقع پروتئینها در آغاز یک ساختار نامشخصی دارند. برای درک بهتر شکل زیر را ببینید که یک پلیپپتاید را قبل و بعد از فرآیند فولدینگ که تبدیل به پروتئین شده است نشان میدهد.

سه سوال مهم ذهن فیزیکدانها رو مشغول کرد و موجب تولد فیزیک پروتئین ها شد.
۱- از نقطه نظر علم فیزیک زنجیرهی آمینواسیدها که پروتئینها رو دیکته میکنند چه حرفی برای ما دارند، آیا با برهمکنش خاصی روبهرو هستیم؟
۲- چطور میتوان فولدینگ را سرعت بخشید؟
۳- آیا الگوریتم کامپیوتری وجود دارد که بتواند ساختار پروتئینها رو از ترتیب آمینواسیدها پیشبینی کند؟
یکی از مهمترین نتایجی که اطلاعات موجودات زنده به ما نشان داده این هست که پروتئینها حرکتهای گرمایی تصادفی دارند. وقتی صحبت از این حرکت میکنیم یعنی مقیاس دیدمون رو کوچک کردیم و میخواهیم ساختار و عملکردی که پروتئینها دارند رو دنبال کنیم. اینجا همون جایی هست که علم بیوفیزیک مولکولی متولد میشود. اما براستی پروتئینها چی هستند؟ در علم بیو به ساختار سه بعدی که از هم به پیوستن آمینواسیدهای یک بعدی درست میشه پروتئین میگویند. فیزیک مساله کجاست؟ بله درسته رفتار کل سیستم مجموع رفتار اجرا نیست. پس یک سیستم پیچیده روبهروی ماست. همه و همه مارو به یک سوال رهنمون میکند. چطور میتوان ساختار پروتئینها رو بر اساس مفاهیم فیزیکی توصیف کرد؟ رمز پاسخ چیزی نیست جز اونی که تو سلولهای بدنمون داریم. دو ویژگی مهم سلولهای بدنمون که در پروتئینها هم میبینیم. پیچیدگی و عدم تقارن اولین راهنمای ما برای مطالعهی فیزیک پروتئینها هستند. اطلاعات موجود در این زمینه نشان میدهد رفتار پروتئینها گاهی بسیار پیچیدهتراز آن چیزی هست که دانشمندان قبلا پیشبینی میکردند. نگاهی کوتاه بیندازیم بر نحوه توصیف پروتئینها:
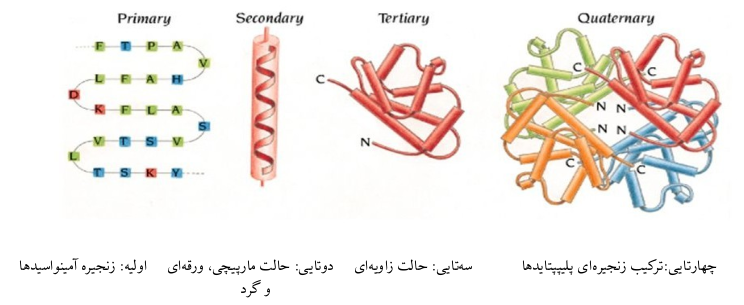
همانطور که در شکل میبینید ساختار کلی به ۴ دسته تقسیم میشود که سادهترین آمینواسیدها هستند و پیچیدهترین ساختار چهارتایی که از به هم پیوستن زنجیرهی پلیپپتایدها تشکیل میشود. اما این جمع شدن چگونه است؟ آیا یک جمع ساده یا یک حرکت جمعی پیچیده؟
امامیخواهیم برگردیم به سه سوالی که در بالا پرسیدیم:
۱– چه ارتباطی بین فیزیکی که ما آموختیم و تاشدگی پروتئین ها وجود دارد؟ بهتره این سوال رو طوردیگری بپرسم. چه مکانیزمی یا فرآیندی وجود دارد که بتواند هدایتگر عمل فولدینگ باشد؟ حالا میتوانیم سوالمون روکمی فیزیکیتر کنیم. چه نیرو یا نیروهایی میتوانند موجب تاشدگی و ایجاد ساختار سه بعدی پروتئینها شوند. شاید شگفتانگیز به نظر بیاید که بانک اطلاعاتی پروتئینها امروزه وجود حدود ۸۰۰۰۰ هزار ساختار پروتئینی رو اعلام میکند که این بسیار شگفتانگیزاست. ساختار پروتئینهای آلفا و بتا در بین خودشون پیوند هیدروژنی دارند و این پیوند وظیفه حفظ ساختار سه بعدی رو دارد.
همچنین در ساختار برخی پروتئینها برهمکنش واندروالسی وجود دارد. جالبه که بدونید پروتئینهای تاشده به شدت در همپکیده هستند و به نوعی ساختار تنگپکیدهای که از فیزیک حالت جامد میشناسیم رو تداعی میکنند. مانند بسیاری دیگر از پلیمرها در انتخاب همسایههاشون ترجیح فضایی دارند. این یعنی هر مونومر آمینواسیدی ممکن است متصل شدن به یک مونومر خاص رو به مونومری دیگر برای تشکیل ساختار پروتئینی رو ترجیح بدهد. پس میتوانیم بگوییم با یک شبکه روبهرو هستیم. بسیاری از آمینواسیدها قابلیت جذب و دقع همدیگر را دارند و این به خاطر برهمکنش الکتروستاتیکی هست که در بین آنها وجود دارد. مجموعهای از این نیروها و بسیاری عوامل خارجی دیگر رو تحت عنوان نیروهای میدانی در فیزیک پروتئینها یاد میکنند که این اجازه رو به ما میدهند تا برهمکنش، دینامیک، نحوه اتصالات و در کل اتفاقاتی که بین پروتئینها جاری است را با مفاهیم فیزیکی توصیف کنیم. نکته جالب اینکه شناخت بسیاری از خواص آماری و ترمودینامیکی پروتئینها هنوز جزئی از مسائل باز فیزیک هستند.
۲- در سال ۱۹۶۸ این سوال پیش آمد که آمینواسیدها علی رغم انتخابهای بسیاری که دارند چرا در کسری از میکروثانیه زنجیره خود را پیدا میکنند و هیچگاه دنبال یافتن و کاوش بیشتر سایر زنجیرههای دیگر نیستند. این سوال منجر به انجام آزمایشهای بسیاری بر روی حرکتشناسی پروتئینها شد به طوری که در این آزمایشات اعلام شد میتوان مسیر فولدینگ پروتيئینها رو پیدا کرد. اما دشواریهای بسیاری پیش روبود. اینکه در ابعاد مولکلول باید دربازههای زمانی میکروثانیه از حرکت پروتئینها عکس گرفت. پس طبعا به ابزار قدرتمند آزمایشگاهی برای این کار نیاز داریم. اما دنبال چه چیزی هستیم. آیا جز اینکه میخواهیم به یک سری خواص این پلیمرها پی ببریم. بله ترمودینامیک آماری پلیمرها در اینجا متولد شد. مطالعهی آنتروپی در زنجیرهی مونومرها و چشم انداز وضعیت انرژی آمینواسیدها ابزار کلیدی ما در شناخت خواص این دسته مواد هستند. اما آیا با همهی این تفاسیر مکانیزم تاشدگی را شناختهایم. اصولا منطورمان از مکانیزم چیست؟ ما به دنبال تحول زمانی آمینواسیدها هستیم تا زمانی که تبدیل به پروتئینهای حلال میشوند. اتفاقات بسیاری ممکن است در این مسیر بیفتد، عوض شدن اتصالات آمینواسیدها، افزایش و کاهش پایداری ساختارها، تغییر مسیر برخی مونومرها با اعمال قیدهایی مثل دمای محیط واینکه در زنجیرهی تشکیل ممکن است برخی مسیرها پرجمعیت تر باشند، پس نمودی از شبکه را بازهم می توانیم احساس کنیم. در کل میخواهم بگویم با یک سیستم کاملا غیرتعادلی روبهرو هستیم. اما راه حل چیست؟ بله حدس شما درست است. آزمایشگاه، دریافت اطلاعات و پردازش اطلاعات با استفاده از کامپیوتر.
۳- اما شاید بزرگترین چالش طراحی کد کامپیوتری جهت پیشبینی ساختار سه بعدی پروتئین باشد. برای این کار جدای از شناخت نسبی کار با کامپیوتر و اطلاعات پروتئینها باید مکانیزم بیولوژیکی آنها رو هم درک کنیم. برای مثال باید درک دقیقی از برهمکنش بین آمینواسیدها داشته باشیم تا بتوانیم آنها رو به بهترین شکل مدل کنیم. خوشبختانه در این زمینه پیشرفتهای بسیاری انجام شده و مهمترین منبعی که میتواند اطلاعات مفیدی در اختیار ما قرار بدهد وبسایت ncbi هست. یکی از مهمترین اتفاقاتی که بعد از سال 1972 افتاد این بود که متخصصان متوجه شدند که ویروسها و باکتریهای حامل آلودگی فقط در بین DNA و RNA گذار نمیکنند. بلکه عامل شیوع برخی بیماریها میتواند پروتئینهای فولد نشده باشند مثل دیابت نوع دو و همچنین آلزایمر و پارکینسون. با توجه به شبیهسازی های اخیر در مورد مدل کردن بیماریها میتوان گفت این نوع دیتا و مدلسازی میتواند موضوع جالبی برای تحقیق و پژوهش باشد. در نهایت میتوانیم بگوییم، هدف پیشبینی ساختار نهایی از زنجیرههای اولیه مونومر هاست. از موضوعات دیگر دینامیک پروتئینها، رفتار جمعی به خصوص در پروتئینهای نامنظم و همچنین تحلیل شبکههای مختلف که از برهمکنش پروتئینها و آمینواسیدها میباشند هستند.
مسائل حل نشده:
مسائل بسیار زیادی در این زمینه و به خصوص بیوفیزیک مولکولی هست که هنوز باز هستند و قابلیت پرداخته شدن دارند. بنا داریم به چندتایی از اونها اینجا اشاره کنیم.
– چشم انداز تجربی هنوز از وضعیت تبادل انرژی بین پروتئینها وجود ندارد.
– هنوز مدل دقیقی برای پیشبینی رفتار پروتئینها ارائه نشده است که دقت بالایی داشته باشد.
– هنوز به طور ریاضی فهمی از رفتار میکروسکوپی آمینواسیدها به طور دقیق حاصل نشده است.
– پیشبینی برای انبوهشدگی پروتئینها که در ایجاد برخی بیماریها مهم است هنوز ارائه نشده است.
– هیچ الگوریتمی هنوز نمیتواند به صورت دقیق وابستگی و همبستگی بین مولکولهای کوچک داروها رو با پروتئینها تبیین کند.
-به طور سیستماتیک هنوز شبکهای از رفتارآمینواسیدها و پروتئینها تدوین نشده است.
– رفتار جمعی پروتئینها در مقیاسهای مختلف میتواند نتایج متفاوتی داشته باشد که هنوز به طور دقیق بررسی نشده است.
این ایده ها و بسیاری ایدههای دیگر همواره میتوانند فرصتی خوب را برای انجام پروژههای علمی مختلف فراهم کنند که البته با توجه به بعد آزمایشگاهی کار برای شروع هر پروژه باید بودجه کافی و متناسب با آن فراهم بشود.
برای آشنایی بیشتر میتوانید به دو مقاله زیر رجوع کنید که البته پایهی اصلی این نوشته نیز میباشند.
منابع:
- The Protein Folding Problem, 50 years on, Science, Vol 338, Issue 6110, Page 1042
- Polymer physics of intracellular phase transitions, nature of physics, 2015
- https://en.wikipedia.org/wiki/Protein_folding
- Biological Physics, Energy, Information, life by Philip Nelson
همچنین در صورتی که خیلی علاقمند به این موضوعات هستید و علاقه دارید یک درس خیلی خوب رو در اینترنت دنبال کنید میتوانید به درس بیوفیزیک مولکولی دانشگاه ایلینوی رجوع نمایید.