این پست، اشاره‌ی مستقیمی دارد به مقاله «استفاده از ساخت‌های نظری برای تدریس آگاهانه» جان میسون که در ۹امین کنفرانس آموزش ریاضی (شهریور ۸۶) ارائه شده. ترجمه مقاله در ۹۳امین شماره مجله «رشد آموزش ریاضی» موجود است.
فرض کنید یک معلم حسابان قصد تدریس مفهوم انتگرال را دارد. قاعدتا راه‌های زیادی برای ورود به مبحث وجود دارد:
روش نخست) معلم برای شروع درس می‌گوید: «انتگرال‌گیری عکس عمل مشتق‌گیری است» و پس از آن لیستی از روابط انتگرال‌گیری برای توابع مختلف ارائه می‌کند و دانش‌آموز هم بدون اینکه دید بیشتری به موضوع پیدا کند، صرفا به خاطر این که از یادداشت کردن مطالب روی تخته جا نماند، سریع شروع به جزوه نویسی می‌کند و لابد بعد از کلاس هم به حفظ کردن روابط می‌پردازد.
روش دوم) کلاس دیگری را فرض کنید که معلم برای شروع درسش به سراغ تخته می‌رود و می‌نویسد: «انتگرال». دانش‌آموز این کلاس که منتظر معرفی این موضوع توسط معلم است با این تعریف ناگهانی از انتگرال مواجه می‌شود که: «انتگرال مقدار مشترک ممکن زیرینۀ مجموعه‌ای ریمانی و زیرینۀ مجموعه‌ای ریمانی یک تابع حقیقی در بازۀ مفروض است. انتگرال از مفاهیم اساسی در ریاضیات است که در کنار مشتق دو عملگر اصلی حساب دیفرانسیل و انتگرال را تشکیل می‌دهند.» و پس از آن هم لابد با تعریف مفاهیمی چون انتگرال معین، انتگرال نامعین و تابع انتگرال‌پذیر مواجه خواهد شد. دانش‌آموز این کلاس، نسبت به کلاس قبل وضعیت اسفناک‌تری خواهد داشت چرا که در کلاس اول دست‌کم فهمیده بود که انتگرال عملیست که با مشتق‌گیری چگونه رابطه‌ای دارد. اما در این کلاس نه تنها با عباراتی مواجه شده که تا کنون دیدی نسبت به آن‌ها نداشته، بلکه رابطه بین مشتق و انتگرال هم دیگر برایش مشهود نیست. خلاصه اینکه این کلاس اگر همین‌گونه پیش‌رود دانش‌آموز فقط گیج و گیج‌تر می‌شود و یادگیری رخ نخواهد داد.
روش سوم) حال، کلاس سومی را در نظر بگیرید که معلم برای شروع از دانش‌آموزان می‌خواهد که مساحت شکل سمت چپ را حساب کنند.
اولین کاری که دانش‌آموزان سراغ آن می‌روند، استفاده از روابط آشنایی است که از هندسه مقدماتی به یاد دارند، اما از آنجا که شکل مذکور مشابه هیچ‌کدام از اشکال آشنا نیست، سراغ قطعه قطعه کردن شکل به اشکال آشنایی چون مستطیل و مثلث می‌روند چرا که می‌توانند مساحت هر جز را اینگونه محاسبه و در نهایت مساحت کل شکل را به دست آورند.
این فرانید چندان طول نمی‌کشد. معمولا دانش‌آموزان به روش‌های مختلفی تقسیم بندی را انجام می‌دهند و در نهایت اکثریت کلاس به یک جواب یکتا می‌رسند. با این وجود، برخی دچار یک‌سری خطا در محاسبه می‌شوند. به عنوان مثال، در محاسبه مساحت یک مثلث، فقط ارتفاع را در قاعده ضرب می‌کنند و این چنین خطاهایی که خودشان سریع متوجه‌شان می‌شوند و معمولا به سرعت هم آن‌ها را اصطلاح می‌کنند. اکنون که معلم دانش‌آموزان را وادار به دست‌ورزی با یک مسئله ساده کرده می‌تواند فراتر رود و شکل را کمی بغرنج کند. یک معلم آگاه می‌داند از این مرحله به بعد هر شکلی که به دانش‌آموزانش بدهد، اولین کاری که آنان برای محاسبه‌ی سطح می‌کنند تقسیم شکل به قطعات قابل محاسبه است. با علم به این موضوع، در مرحله بعد، معلم از دانش‌آموزان می‌خواهد که مساحت سطح زیر یک منحنی را محاسبه کنند. اینجاست که دانش‌آموزان دچار یک نگرانی می‌شوند.
آن‌ها نمی‌توانند سطح مورد نظر را با تعداد مشخصی از اشکال آشنا بپوشانند. چرا که آن‌ها یا سطح را کامل نمی‌پوشانند یا اینکه قطعاتشان بزرگتر از سطح از آب در میاند. به همین دلیل، در این مرحله، بر خلاف قسمت قبل، اکثریت کلاس برای شروع مسئله حدس‌های مختلفی می‌زنند. در نهایت، دانش‌آموزان به یک جواب یکتا نمی‌رسند و هر کس برای خود جوابی دارد که احتمالا ادعا هم می‌کند که پاسخش صحیح‌ترین است. کاری که یک معلم آگاه در این شرایط انجام می‌دهد این است که از دانش‌آموزان بخواهد روششان را توضیح دهند و دلیل بیاورند که چرا این روش صحیح است. همین‌طور اگر کسی ادعا دارد که روش دوستش نادرست است، علتش را بیان کند، به نحوی که بتواند کلاس و معلم را متقاعد سازد. در حقیقت، در این شرایط تمام جر و بحث‌هایی که بر سر صحت پاسخ‌ها صورت می‌گیرد، صرف نظر از خطاهای محاسباتی، بر سر چگونگی پر کردن فضای زیر منحنی توسط اشکال هندسی آشناست. در میان بحث و گفتگوی صورت گرفته بین دانش‌آموزان با معلم و دانش‌آموزان با یک‌دیگر، کم‌کم مشخص می‌شود که هیچ جوابی کاملا صحیح نیست و در واقعا هر چه دقیق‌تر سطح زیر منحی با اشکالی که مساحتشان قابل محاسبه است پوشانده شود، عدد به دست آمده صحیح‌تر است. در این جاست که دانش‌آموزان با مفهوم تقریب و تقریب زدن آشنا می‌شوند. پس قدم بعدی برای معلم، هدایت دانش‌آموزان به سمت محاسبه‌ی سطح زیر منحنی با تقریب بهتر و نزدیک‌تر به جواب دقیق است. از آنجا که در برنامه آموزشی، مفهوم سری‌های هم‌گرا و حد یک دنباله قبل از انتگرال به دانش‌آموزان معرفی می‌شود، معلم به راحتی می‌تواند مسیر فکری دانش‌آموزان را به این سمت ببرد که آن‌ها می‌توانند مستطیل‌های زیادی کنار هم بگذراند به طوری که عرض آن‌ها را هرچقدر که می‌خواهند کوچک‌در نظر بگیرند و در نهایت با جمع کردن این مستطیل‌ها بتوانند با تقریب خوبی مساحت را به دست‌بیاورند. اینجاست که معمولا دانش‌آموزان – که حسابی در فرایند دست‌ورزی با مسئله گرم شده‌اند- به وجد می‌‌آیند و به معلم می‌گویند ما می‌توانیم با جمع کردن بی‌شمار مستطیل که عرضشان را بسیار کوچک گرفته‌ایم سطح را به طور کامل بپوشانیم.
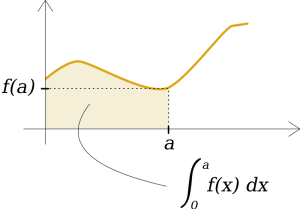
معلم هم که از قبل تمام این سناریو را چیده بود، از آن‌ها می‌خواهد تا حرفی که زدند را دقیق‌تر بیان کنند. به عبارت دیگر معلم به کمک دانش‌آموزان شروع به نوشتن تمام داستان به زبان ریاضی (استفاده از نمادگذاری ریاضی) می‌کند تا اینکه سطح مورد نظر را به طور دقیق اندازه‌گیری کند. در انتها معلم به دانش‌آموزان می‌گوید: «به کاری که ما امروز در کلاس انجام دادیم، یعنی محسابه‌ی سطح زیر یک منحنی، انتگرال‌گیری می‌گویند.» و ادامه ماجرا…
مسلما در کلاس‌های بالا، میزان یادگیری متفاوت است. کدام روش بهتر است؟ مسلما هر کسی ترجیح می‌دهد دانش‌آموز آخرین کلاس باشد. ماجرا از اینجا شروع می‌شود که یادگیری را می‌توان ترکیبی از تکلیف، فعالیت، تجربه و بازتاب دانست. تکلیف معمولا یک یا چند مسئله است که می‌تواند شروع یک فعالیت در کلاس باشد. درست مانند آنچه که در ابتدای کلاس سوم (مساحبه مساحت چهارضلعی) رخ داد. معمولا تکلیف هیچ‌گاه قبل از شروع تدریس وجود ندارد. مدرس یا از آن برای شروع یک مطلب استفاده می‌کند و یا پس از تدریس خود تکلیفی برای دانش‌آموز مشخص می‌کند که آن‌را انجام دهد. معمولا تکالیف در کتاب‌های درس مشخص شده‌اند. در مثال ما، پس از تکلیف، یک فعالیت در کلاس رخ داد. فعالیت، یک فرایند چالش‌برانگیز است که در آن دانش‌آموز با توجه به دانسته‌های قبلی و توانمندی‌های خود، تحت هدایت معلم، با یک مسئله جدید آشنا می‌شود.
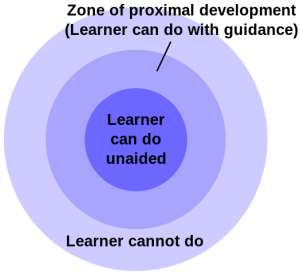
در حین فعالیت، دانش‌آموز سعی بر توسعه ابزارهای مورد نیاز برای حل مسئله (تکلیف) می‌کند. در حقیقت فعالیت مجموعه‌ای از اقداماتی است که یادگیرنده با وجود داشتن دانش در آن حیطه، به کمک یک یاددهنده آن‌ها را پیش می‌برد (دامنه تقریبی رشد). در کلاس اول و کلاس دوم، هیچ گونه فعالیتی در کلاس صورت نگرفت. دانش‌آموزان فقط با یک دسته تعریف و یا رابطه روبه رو شدند که نمی‌توانستند ارتباط منطقی بین آنچه در آن جلسه در کلاس درس می‌دیدند با دانسته‌های قبلی خود برقرار سازند. بر خلاف کلاس سوم، دانش‌آموزان به هیچ‌وجه وادار نشدند که از توانایی‌های طبیعی مختلف‌شان در زمان کلاس برای یادگیری استفاده کنند. از طرف دیگر، هنگامی که دانش‌آموز مجبور شود پشت جزوه‌اش مخفی شود و منتظر باشد تا استاد مطلب را بگوید و او یادداشت کند یا اینکه تمام تلاشش این باشد که در نهایت الگوی مشابهی بین مثال‌های حل شده بیابد که به کمک آن به سوالات امتحان پاسخ‌دهد، هیچ‌گاه تفکر ریاضی در او رشد نخواهد کرد. در کلاس سوم، در حین فعالیت، دانش‌آموزان این فرصت را داشتند که حدس بزنند (در مورد چگونگی پرکردن فضاهای خالی)، آن‌ها حتی این فرصت را داشتند که حدس اشتباه بزنند و پس از آن اشتباه خود را تصحیح کنند و از اشتباه خود بیاموزند. معلم آگاه، به پاسخ دانش‌آموز باید به منزله یک حدس نگاه کند، حدسی که در صورت ناقص بودن نیاز به تکمیل و در صورت نادرست بودن نیاز به تصحیح دارد. نکته‌ی بسیار قابل توجه این است که «برای شکوفایی تفکر ریاضی، ضروی است که فضای کلاس درس، فضای حدس باشد.» ویژگی دیگر کلاس سوم این بود که دانش‌آموزان توانستند با استفاده از دانسته‌های قبلی خود (مفهوم حد، سری و همگرایی) به یک مفهوم جدید (انتگرال) برسند که در حقیقت تعمیمی از همان اندازه‌گیری مساحت بود که قبلا برای شکل‌های خاص می‌توانستند حساب کنند. در صورتی که در دو کلاس اولی چنین چیزی وجود نداشت. دانش‌آموزان کلاس سوم، خود را مالک و خالق ریاضیاتی می‌دانند که تا آن لحظه آن را ساخته‌اند در صورتی که این ریاضیات برای دانش‌آموزان کلاس اول و دوم به منزله‌ی یک فرزند سر راهی است؛ آن‌ها هیچ حسی نسبت به آن ندارند! به قول جان میسون: «درسی که به یادگیرندگان هیچ فرصتی نمی‌دهد که فرایند تعمیم را تجربه کنند یک درس ریاضی نیست!». مسلما دانش‌آموزان کلاس سوم می‌توانند با ابزاری که اکنون به اسم انتگرال‌گیری در دست دارند به سراغ مثال‌های قدیمیشان روند و اندازه مساحتشان را با توجه به رهیافت جدید به دست آورند که این خود بخشی از فرایند ریاضی‌فکر کردن است (doing and undoing).
نکته‌ای کلیدی در مورد فعالیت وجود دارد و آن اینکه، فعالیت، یادگیری نیست! با این وجود، در مسیر فعالیت یادگیری می‌تواند صورت گیرد. چیزی که در کلاس سوم فعالیت را به یادگیری تبدیل کرد تجربه و بازتاب بود. به عنوان مثال، در کلاس سوم برای محاسبه‌ی سطح زیر منحنی دانش‌آموزان از اشکال مختلفی با اندازه‌های متفاتی و چینش گوناگونی استفاده کردند که برای هر کسی یک تجربه قلمداد می‌شود. از سوی دیگر، در طی فعالیت، ممکن است یادگیرنده اقدامات پراکنده‌ای انجام دهد که لزوما همه آن‌ها مرتبط با مسیر آموزشی نباشد، بنابراین وظیفه‌ی معلم هدایت تجربه‌های دانش‌آموزانش است. هدایت به سمتی که تجربه‌ها به کارآیند! معلم در مسیر آموزش، تجربه‌ی دانش‌آموزان را به وادی ارزشیابی می‌برد. در کلاس سوم، معلم پس از آنکه به یادگیرندگان فرصت کافی برای کسب حس معنادار از چگونگی حل مسئله داد، از آن‌ها خواست تا به یک نتیجه برسند، به عبارتی تفسیرهای خود را از فعالیتی که انجام داده‌اند بیان کنند. برخلاف کلاس اول و دوم، در کلاس سوم ابتدا دانش‌آموزان شروع به دست‌ورزی به مسئله کردند تا اینکه تحت هدایت معلم به یک حس معنادار رسیدند به طوری که در نهایت توانستد نتیجه‌ی کار خود را به صورت دقیق بیان کنند (MGA). دانش‌آموزی که از مفهوم ساده‌ی جمع و اندازه‌گیری مساحت به شیوه‌ای کاملا ابتدایی به محاسبه حد یک سری می‌رسد، پی به زیبایی و نظام‌بندی ریاضی می‌برد. چیزی که به کمک آن توانسته از یک مفهوم ساده، یک مفهوم تعمیم یافته جدید بسازد و آن را بیان کند. ممکن است یادگیرندگان بیان‌ها و تفاسیر مختلفی از یک موضوع را ارائه دهند. اینجا معلم وارد عمل می‌شود و باز هم به کمک خود دانش‌آموزان سعی به رسیدن به صحیح‌ترین و دقیق‌ترین و موجزترین بیان ممکن می‌کند. بنابراین اگر معلم کلاس سوم، تعبیر معلم کلاس دوم را در انتهای کلاسش مطرح کند، احتمالا با چشم‌هایی درشت شده و سرهای شاخ در آورده از تعجب مواجه نخواهد شد، چرا که دانش‌آموزان در کلاس سوم هم تلاش برای دست‌ورزی و رسیدن به روابط معنادار کردند و هم در حین گفتگوها ایده‌های یکدگیر را به چالش کشیدند و در نهایت هم به کمک همدیگر، تحت رهبری و هدایت، به یک جمع‌بندی رسیده‌اند (DTR).
آنچه که در انتها باید به آن اشاره شود این است که تدریس و یادگیری دو فرایند متفاوت هستند.
